1. Алгебра
  2. Решите неравенствов ответе

Решите неравенство

в ответе получается (3; 4); (4; 5]
у меня не сошлось с ответом

annyakristina annyakristina    1   01.10.2019 11:16    3

Ответы
andrey5890 andrey5890  09.10.2020 07:39

\log_9(x-3)\cdot \log_{x-3}(x+4)- \log^2_9(x+4)\geq 0

Рассмотрим функцию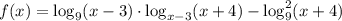 f(x)=\log_9(x-3)\cdot \log_{x-3}(x+4)- \log^2_9(x+4). Ее область определения:

\begin{cases}&\text{}x-30\\&\text{}x-3\ne 1\\&\text{}x+40\end{cases}~~~\Rightarrow~~~\begin{cases}&\text{}x3\\&\text{}x\ne 4\\&\text{}x-4\end{cases}~~~\Rightarrow~~~ x \in (3;4)\cup (4;+\infty)

Решим уравнение f(x) = 0

\log_9(x-3)\cdot \log_{x-3}(x+4)- \log^2_9(x+4)=0\\ \\ \log_9(x-3)\cdot \dfrac{\log_9(x+4)}{\log_9(x-3)}-\log^2_9(x+4)=0\\ \\ \log_9^2(x+4)-\log_9(x+4)=0\\ \\ \log_9(x+4)\left(\log_9(x+4)-1)=0

Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю

\left[\begin{array}{ccc}\log_9(x+4)=0\\ \\ \log_9(x+4)-1=0\end{array}\right~~~\Rightarrow~~~\left[\begin{array}{ccc}x+4=1\\ \\ x+4=9\end{array}\right~~~\Rightarrow~~~\left[\begin{array}{ccc}x_1=-3\\ \\ x_2=5\end{array}\right

(3)____+__(4)___+____[5]______-_______>

ответ: x ∈ (3;4)∪(4;5]

ПОКАЗАТЬ ОТВЕТЫ
KatherinePirs KatherinePirs  09.10.2020 07:39

ответ и решение во вложении


Решите неравенствов ответе получается (3; 4); (4; 5]у меня не сошлось с ответом
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
12365874 12365874  25.02.2021 16:58
На каком из рисунков прямые будут параллельны? Поясните свой ответ. ​...
Гыгыгы14 Гыгыгы14  25.02.2021 16:59
— x РешиСколько кубиков нужноубрать из фигуры А, чтобыполучить фигуру Б?Чему равна неизвестная часть?AБ— x-AБ​...
Dailll Dailll  25.02.2021 17:00
10x3+x2+10x+1, если x=0,3​...
djgas10 djgas10  25.02.2021 17:01
Если (а-b)² =64и ab =3 то найдите значения выражения (a+b)²​...
shavkatbronduk1 shavkatbronduk1  03.12.2020 10:59
Найдите значение выражение log₂a, если log₃₂a=2.​...
Анетта666 Анетта666  03.12.2020 10:59
Можно решение с 16,29-16,43(нечётные задания) ​...
Semensem Semensem  03.12.2020 10:58
Выразите: а) в дм. 75000мм; 340см; 5м​...
Kirill15003 Kirill15003  03.12.2020 10:58
решить контрольную по алгебре >...
anastasiabobilevich anastasiabobilevich  03.12.2020 10:58
Ребята умоляю не понимаю ничего...
eldarsorokin2 eldarsorokin2  23.02.2022 03:41
решить (( a) x²y²(x + y); б) -p⁵q⁸(p³ + 3pq - q⁴); в) -c³d⁴(c² - d³); г) r⁷s¹²(r¹⁰ + 2rs - s⁵)....

Популярные вопросы