1. Алгебра
  2. Решите неравенствоf (x)⩾0

Решите неравенство
f'(x)⩾0
y = 1/3x³-x²-8x-1

ванёк10062005 ванёк10062005    3   08.02.2022 20:19    0

Ответы
hanter13 hanter13  08.02.2022 20:20

Пользуемся формулами:

\boxed{\ (u\pm v)'=u'\pm v'\ \ \ ,\ \ (x^{n})'=nx^{n-1}\ \ ,\ \ (Cu)'=Cu'\ }y=\dfrac{1}{3}\, x^3-x^2-8x-1\ \ ,\ \ \ f'(x)\geq 0\ \ ,y'=\dfrac{1}{3}\cdot 3x^2-2x-8\ \ ,\ \ \ x^2-2x-8\geq 0

Корни квадратного трёхчлена найдём по теореме Виета, это будут числа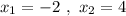   x_1=-2\ ,\ x_2=4  .

Разложим левую часть неравенства на множители.

(x+2)(x-4)\geq 0

Hешим неравенство методом интервалов . Отметим нули функции на оси и расставим знаки в образовавшихся интервалах.

  +++[-2\ ]---[\ 4\ ]+++  .

Выбираем знак плюс .

x\in (-\infty \, ;-2\ ]\cup [\ 4\ ;+\infty \, )

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
xandias xandias  18.06.2019 01:30
Решите уравнение sin(t-10pi)+ 2sin(t+4pi)=3...
Sumiya666 Sumiya666  18.06.2019 01:30
Вынесите множитель за знак корня: а) √45 ; б) √396 ; в) √176 ; г) √1100 ; д) 0.2√2475 ; е) 0,3√300 ; ж) −0.125√1792 ; з) −3/2√117 ; ....
матеки матеки  18.06.2019 01:30
Автобус едет от одного города до другого со скоростью 50 км/ч, а автомобиль-со скороcтью 80 км/ч, и весь путь занимает у него на 1.5 ч меньше, чем у автобуса. определите...
csmos csmos  18.06.2019 01:30
Постройте график уравнения (х^2+у^2-8х)(х+у)=0 фото...
lewaq lewaq  18.06.2019 01:30
Докажите,что функция f(x) = 2x в кубе + sin x является нечетной ....
marybyl86 marybyl86  18.06.2019 01:30
Запишите выражение в виде многочлена: а) (а+5)^2. в) (х-2)^3 б) (а+6)(а-6). г) (х+3)(х^2-3х+9)...
LymarIvan LymarIvan  18.06.2019 01:40
Сравните значения выражений: а) 4√3 и √9 ; б) √21 и 3√8 ; в) 5√4 и 4√5 ; г) 2√7 и 2√2 ; д) −√14 и −3√3 ; е) −10√0.17 и −11√0.05...
t89633261566polypony t89633261566polypony  18.06.2019 01:40
При каком значении c график функции y=x^2-6x+c 1)проходит через начало координат 2)имеет с осью абсцисс только одну общую точку 3)пересекает ось ординат в точке...
juliakovta juliakovta  18.06.2019 01:40
Lim ( x стремится к бесконечности) (1-1/t)^t...
tukacheva88 tukacheva88  18.06.2019 01:40
:семь досок и три кирпича вместе весят 71 кг. три доски тяжелее двух кирпичей на 14 кг. сколько весит одна доска и один кирпич?...

Популярные вопросы