Решите неравенство с объяснениями 36^x-1/2-7 * 6^x-1 +1 >=0

хє (-∞;0] U [1;+∞)

Объяснение:

пусть 6^(х-1)=а >0

тогда

36^(х-1/2)=36^(х-1+1/2)=

=36^(х-1)*36^(1/2)=6^2^(х-1)*√36=

=(6^(х-1))^2 * 6

→

36^(x-1/2) - 7*6^(x-1) +1 ≥0 ←→

(6^(х-1))^2 * 6 - 7*6^(x-1) +1 ≥0 ←→

а^2 * 6 - 7 * а + 1 ≥ 0

или 6а² -7а+1≥0

Д = (-7)²-4*6*1=49-24=25=5²>0

а1=(7+5)/(6*2)=12/12=1

а2=(7-5)/(6*2)=2/12=1/6

6а² -7а+1≥0 ←→ 6*(а-1)(а-1/6)≥0

+. -. +

••›

1/6. 1. а

а є (-∞;1/6] U [1;+∞)

с учётом одз (а>0) получаем:

а є (0 ;1/6] U [1;+∞)

Выход из замены:

1) а>0 и а≤1/6, а=6^(х-1)

а>0 (при любом х)

а≤1/6 → 6^(х-1)≤1/6

6^(х-1)≤6^(-1)

6>1 → х-1≤-1

х≤0

2) а≥1, а=6^(х-1)

6^(х-1)≥1

6^(х-1)≥6^0

6>1 → х-1≥0

х≥1

Объединяя получаем:

хє (-∞;0] U [1;+∞)

Теория:

Объяснение:

;

;

;

;

Пусть , тогда

;

;

Решением этого неравенства является промежуток t∈(0;1]U[6;+∞)

Вернёмся к замене:

Если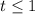 , то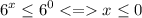

(Т.к. по определению любое число в степени строго больше нуля, то мы можем не писать )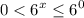

Если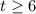 , то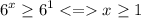

ответ: х∈(-∞;0]U[1;+∞)