Решите неравенство: log0,5 (3x-1)-log0,5 (x-1)
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкаком слове нет суффикса! лучик, пончик, тортик, зонтик....
2 - Пять молей ионов образуется при полной диссоциации одного моля:...
3 - 3.выбери и обведи нужную букву 1) вilly… got many sweets on the...
3 - Нужно составить 25 реакций для азота и его соединений...
3 - Прочитай признания в.и.белова. как ты понимаешь эти слова писателя?...
2 - Можете правильно перевести предложения на язык , . 1)я—сирота....
2 - При сжигании 18 г вещества получили 13,44 литров co2 и 10,8 г h2o...
3 - Это с дробями и вместо тире тоесть этот символ - запятая будет...
2 - Вцистерне, заполненной нефтью, на глубине 4м поставлен кран. определите...
3 - Придумайте рифмы к строчкам или допишите стих на тему не ходи по...
3
{3x-1>0⇒x>1/3
{x-1>0⇒x>1
{x+18>0⇒x>-18
{x+2>0⇒x>-2
x∈(1;∞)
log(0,5)[(3x-1)/(x-1)]<log(0,5)[(x+18)/(x+2)]
(3x-1)/(x-1)>(x+18)/(x+2)
(3x-1)/(x-1)-(x+18)/(x+2)>0
(3x²+6x-x-2-x²-18x+x+18)/[(x-1)(x+2)]>0
(2x²-12x+16)/[(x-1)(x+2)]>0
2(x²-6x+8)=0
x1+x2=6 U x1*x2=8⇒x1=2 U x2=4
x-1=0⇒x=1
x+2=0⇒x=-2
+ _ + _ +
(-1)(1)(2)(4)
x∈(1;2) U (4;∞)
ОДЗ:
+ - +
-------------(2)-------------(4)-------------
//////////////// ////////////////
С учётом ОДЗ получаем
ответ: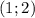 ∪
∪ 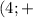 ∞
∞ 