Решите неравенство 9 в степени х - 3 в степени х - 6 > 0

9^x - 3^x - 6 > 0

3^2x - 3^x - 6 > 0

замена

3^x = y

ОДЗ: у > 0

y² - y - 6 > 0

найдём нули функции  f(y) = y² - y - 6

решим уравнение y² - y - 6 = 0

D = 1 + 24 = 25

√D = 5

y₁ = (1 - 5):2 = -2

y₁ = (1 + 5):2 = 3

График функции f(y) = y² - y - 6  квадратная парабола веточками вверх, поэтому неравенство y² - y - 6 > 0 имеет решение у∈(-∞; -2)U (3; +∞)

c учётом ОДЗ получаем у∈(3; +∞)

вернёмся к замене

3^x = 3

х = 1

ответ: х∈(1; +∞)

Так как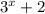  больше нуля при всех значениях x, то нам необходимо только найти при каких значениях x выражение 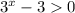. Ее легко решить и получить что x>1