Решите неравенство √(2x²-8x+6) + √(4x-x²-3) <x-1
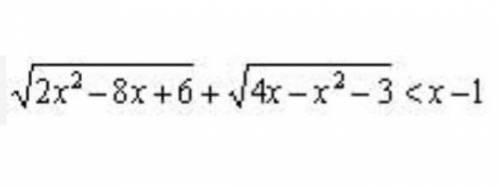
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему граждане афин могли учавствовать в государством?...
3 - Какова молярная концентрация раствора, содержащего 0,3 моль хлорида натрия...
2 - 80000мм² в см² ? я вопще не знаю сколько будет бьюсь бьюсь а не могу!...
2 - 20 .задайте формулой линейную функцию, если известно что ее график проходит...
1 - 1) почему глав. герой начал играть на деньги.2) как вёл себя во время драки....
3 - (не понимаю, 6 кл) самая низкая температура воздуха, зафиксированная в пустыне...
2 - Написати програмний код процедури для обчислення суми чисел, кратних 5, з...
1 - Найти площадь фигуры? которая задается на координатной плоскостями условиями...
2 - Записать словами числительные: 1) к 14 прибавить 75, 2) с 47 сложить 68,...
2 - Луч bd проходит между сторонами уга abc.нaйдите угол dbc, если угол abc=63...
1
Шаг 1: Определите область допустимых значений
Для неравенства, содержащего корни, мы должны учесть ограничения на выражения под корнем. Так как в обоих корнях есть знак меньше, мы должны установить, что выражения под корнями должны быть положительными.
2x²-8x+6 > 0
4x-x²-3 > 0
Шаг 2: Решите неравенства под корнями
Давайте начнем с первого неравенства:
2x²-8x+6 > 0
Мы можем посмотреть на дискриминант этого уравнения, чтобы определить его корни. Дискриминант вычисляется как D = b²-4ac, где в уравнении ax²+bx+c = 0 коэффициенты a, b и c:
D = (-8)² - 4(2)(6) = 64 - 48 = 16
Поскольку дискриминант положительный, у нас есть два различных действительных корня. Мы можем использовать кривизну этого уравнения для определения того, когда оно больше нуля или меньше нуля.
Мы знаем, что а = 2, поэтому парабола открывается вверх. Поэтому функция будет положительной между корнями.
Давайте найдем корни, используя квадратное уравнение:
x = (8 ± √16) / 4
x1 = (8 + 4) / 4 = 12 / 4 = 3
x2 = (8 - 4) / 4 = 4 / 4 = 1
Таким образом, у нас есть два корня: x = 3 и x = 1.
Теперь мы можем построить таблицу знаков, чтобы определить, когда выражение 2x²-8x+6 будет положительным:
| x < 1 | 1 < x < 3 | x > 3 |
--------------------------------
| - | + | + |
--------------------------------
Переходим ко второму неравенству:
4x-x²-3 > 0
Дискриминант:
D = 1² - 4(1)(-3) = 1 + 12 = 13
Также положительный дискриминант, значит у нас есть два корня:
x = (1 ± √13) / 2
Мы можем продолжить и использовать таблицу знаков, но мы можем также сразу найти значения выражения для x < 1, 1 < x < 3 и x > 3.
Если x < 1, то значение выражения 4x-x²-3 будет положительным. Например, если x = 0:
4(0) - (0)² - 3 = -3
Если 1 < x < 3, то значение выражения 4x-x²-3 будет отрицательным. Например, если x = 2:
4(2) - (2)² - 3 = 8 - 4 - 3 = 1
Если x > 3, то значение выражения 4x-x²-3 будет снова положительным.
Шаг 3: Определите, когда левая сторона неравенства меньше x-1
Чтобы определить этот момент, мы можем рассмотреть различные интервалы значений x, которые нам известны после шага 2.
Если x < 1, то левая сторона неравенства всегда будет меньше x-1, так как мы видели в шаге 2, что это выражение отрицательно для всех значений x < 1.
Если 1 < x < 3, то мы должны сравнить значение левой стороны неравенства с x-1:
Берем значение x = 2:
√(2(2)²-8(2)+6) + √(4(2)-(2)²-3) = √(8-16+6) + √(8-4-3) = √(-2) + √(1) = Неопределено
Мы получили неопределенность, что означает, что в данном интервале неравенство не имеет решений.
Наконец, если x > 3, то левая сторона неравенства снова меньше x-1. Так как из таблицы знаков мы видели, что выражение под корнем и само выражение всегда положительно для значений x > 3.
Итак, мы получили несколько интервалов, где неравенство выполняется:
x < 1 и x > 3.
Итак, ответ на неравенство √(2x²-8x+6) + √(4x-x²-3) <x-1: x < 1 или x > 3.