1. Алгебра
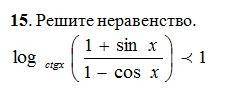
  2. Решите неравенство............

Решите неравенство............


Решите неравенство............

Фиалка2017 Фиалка2017    2   13.07.2020 22:13    0

Ответы
cool589 cool589  30.08.2020 13:15

Применяя метод рационализации получаем систему:

{ctgx >0⇒ x∈ (πm; (π/2)+πm), m∈Z

{(1+sinx)/(1-cosx) >0⇒  x≠(-π/2)+2πk, x≠2πn, k, n ∈Z

{(ctgx-1)·((1+sinx)/(1-cosx)  - ctgx ) <0

Решаем третье неравенство системы:

(\frac{cosx}{sinx}-1)\cdot (\frac{1+sinx}{1-cosx} - \frac{cosx}{sinx})

Решаем методом интервалов.

Находим нули числителя:

cosx-sinx=0    или        sinx-cosx+1=0    вводим вс угол

tgx=1                   или      \frac{1}{\sqrt{2}} cosx-\frac{1}{\sqrt{2}}sinx=\frac{1}{\sqrt{2}}

x=\frac{\pi }{4} +\pi t, t\in Z   или     x+\frac{\pi }{4}=\pm\frac{\pi }{4}+2 \pi s, s\in Z  не входят в ОДЗ

Находим нули знаменателя:

1-cosx=0         или    sinx=0

x=2\pi n, n\in Z    или  x=\pi k, k \in Z

(0) __+__ (π/4)___-__ (π/2)

При х=π/6

\frac{(cos\frac{\pi }{6} -sin\frac{\pi }{6})(sin\frac{\pi }{6}-cos\frac{\pi }{6}+1)}{(1-cos\frac{\pi }{6})sin^2\frac{\pi }{6}} 0

При х=π/3

\frac{(cos\frac{\pi }{3} -sin\frac{\pi }{3})(sin\frac{\pi }{3}-cos\frac{\pi }{3}+1)}{(1-cos\frac{\pi }{3})sin^2\frac{\pi }{3}}

О т в е т.( (π/4)+πn; (π/2)+πn), n∈Z

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
7547854 7547854  24.02.2022 10:29
Как решить неравенство x^2-81 0,при-бесконечность до +бесконечность,и -9 до + бесконечность?...
ksusha020504 ksusha020504  10.04.2020 14:02
решить, не только ответ а еще и решение...
superg64745 superg64745  10.04.2020 14:02
Вычисли угол ASB, если градусная мера дуги ASB равна 289°. Угол ASB=...
1234567311 1234567311  10.04.2020 14:02
с контроольной Під яким порядковим номером число 256 належить геометричній прогресії в якої , b1=4 q=2?...
павел412 павел412  10.04.2020 14:02
Сложи почленно неравенства 17 22 и −0,9 −3,4.​...
муратдавлетов муратдавлетов  10.04.2020 14:02
Вынеси множитель из-под знака корня: корень из 50....
yuraseven77 yuraseven77  10.04.2020 14:01
Решить квадратные уравнения: 4x2 + 6x + 2 = 0...
илона2707 илона2707  10.04.2020 14:01
В прямоугольном треугольнике один из катетов на 7 см больше другого найдите катеты треугольника если его гипотенуза 13 см...
damirnikiforov damirnikiforov  10.04.2020 14:01
Y=ax2+bx+c. Сопоставить графики функций и коэффициенты...
ангел809 ангел809  05.05.2020 10:45
Х^2+x-12 0 квадратные неравенства...

Популярные вопросы