Алгебра: Решите неравенство 1/х-1+1/2-х =5

Решите неравенство 1/х-1+1/2-х< =5

Ответы

натали200652 07.10.2020 13:00

$\dfrac{1}{x-1}+\dfrac{1}{2-x}-5\leq0$

Рассмотрим функцию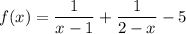 $f(x)=\dfrac{1}{x-1}+\dfrac{1}{2-x}-5$ .

Найдем область определения функции: функция существует, когда знаменатель дроби не обращается в ноль

$\displaystyle \left \{ {{2-x\ne0} \atop {x-1\ne0}} \right. ~~~\Rightarrow~~~~\left \{ {{x\ne2} \atop {x\ne 1}} \right.$

$D(f)=(-\infty;1)\cup(1;2)\cup(2;+\infty)$

Найдем теперь нули функции:

$\dfrac{1}{x-1}+\dfrac{1}{2-x}-5=0~~~~\bigg|\cdot (x-1)(2-x)\\ \\ 2-x+x-1+5(x-1)(x-2)=0\\ \\ 1+5(x^2-3x+2)=0\\ \\ 5x^2-15x+11=0\\ \\ D=(-15)^2-4\cdot5\cdot11=5\\ \\ x_{1,2}=\dfrac{15\pm\sqrt{5}}{10}$

ответ: $x \in \bigg(-\infty;1\bigg)\cup\left[\dfrac{15-\sqrt{5}}{10};\dfrac{15+\sqrt{5}}{10}\right]\cup\bigg(2;+\infty\bigg)$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

VetaRo 08.12.2020 04:08

В квадратном уравнении укажите коэффициенты: -3 x^2+10x+5=0...

Мерлинbrother2 08.12.2020 04:09

Найдите область определения функцииу=__1__ (3-2х)²...

bubo4ka995 08.12.2020 04:10

решить данный вопрос который понадобится в ближайшее время, а точнее завтра...

КатаринаВаулина 27.08.2019 21:00

Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки,затем присвоили к берегу и,погуляв 3 часа,вернулись обратно через 7 часов от начала путешествия.на...

alaaaaaaa 27.08.2019 21:00

Впрогрессии bn известно, что b4=16, b7=1024. найдите знаменатель прогрессии....

Топовыйшкольник 27.08.2019 21:00

При каком значении k график функции y=kx-15 проходит через точку c (-2; -3)? !...

Макс777333 27.08.2019 21:00

Нужно составить график уравнения, но его я сделаю сама просто найти точки для этого графика ( решить уравнение) x - 2y = -2...

Yarik346 27.08.2019 21:00

Решить уравнения для 7 класса x(x^2-16)= 0; x^2-x=0; 3x^2-27=0, !...

valeriehunt 27.08.2019 21:00

(3х-1)(3х+-2)²=0 решить уравнение !...

тина123болото 27.08.2019 21:00

Сократить дробь 9a^2-6a+1 6a^2+a-1...

Решите неравенство 1/х-1+1/2-х< =5

Популярные вопросы