1. Алгебра
  2. Решите неравенство 0 class=

Решите неравенство
0 " class="latex-formula" id="TexFormula1" src="https://tex.z-dn.net/?f=%20%7B3%7D%5E%7B%20%5Csqrt%7B1%20-%20x%7D%20%7D%20-%20x%20log_%7B5%7Dx%3E%200%20" title=" {3}^{ \sqrt{1 - x} } - x log_{5}x> 0 ">
​

dhgti dhgti    1   28.02.2020 01:35    1

Ответы
matvak matvak  11.10.2020 15:03

3^{\sqrt{1 - x}} - x\log_{5}x 0

Найдем область допустимых значений (ОДЗ):

\left\{\begin{array}{ccc}1 - x\geq 0\\x 0 \ \ \ \ \ \\\end{array}\right

\left\{\begin{array}{ccc}x \leq 1\\x 0 \\\end{array}\right

Следовательно, x \in (0; \ 1]

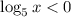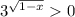Так как \log_{5}x < 0 при x \in (0; \ 1] , а 3^{\sqrt{1 - x}} 0, делаем вывод: данное неравенство выполняется при всех значениях x из области допустимых значений.

ответ: x \in (0; \ 1]

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Nickky Nickky  22.04.2020 12:28
У = -6х + b. График этой функции проходит через точку А(2;-9). Найдите b у = 0,7х - 3,5. Найдите координаты точки пересечения графика этой функции с осью абсцисс...
kristya0414 kristya0414  22.04.2020 12:28
Найдите общую площадь по схеме...
mmb1 mmb1  22.04.2020 12:28
с алгеброй.Найдите область определения функции.​...
Gotaur Gotaur  22.04.2020 12:28
Построй график уравнения Икс плюс игрек равно 5 игрек минус 4 икс равно 0,6 икс равно 4,8 0,5=1,5​...
samira2314 samira2314  22.04.2020 12:28
Решите неравенство: (2 – х )(х + 3) ≥ 0 *(-∞; -3)∪(2; +∞)(-∞; -2)∪(3; +∞)(-∞;-3]∪[2; +∞)(-∞;-2]∪[3; +∞)(х – 2)^2(х + 1) 0 *(-∞;-1]∪[2; +∞)(-1;2)∪(2; +∞)(-∞;-2]∪[1; +∞)(-∞;-2)∪(1;...
zherukova00 zherukova00  22.04.2020 12:28
Найдите моду, медиану и среднее арифметическое ряда, представленного таблицей частот....
775645 775645  22.04.2020 12:28
Дана функция Найдите: 1) f (-2); 2) f(-1); 3) f(2); 4) f(4); 5) f(4,1)/ ответы запишите через точку с запятой без пробелов и нумерации....
вика3169 вика3169  22.04.2020 12:28
АЛГЕБРА 8 КЛАСС!Нужно определить значения выражения...
Daniil3037 Daniil3037  22.04.2020 12:28
Решите систему уравнения методом подстановки...
Kazybek0611 Kazybek0611  22.04.2020 12:28
586. Решите неравенство:(х + 2)(х - 4) .(х+3)хх? + 4х +7х? – 6х + 5б) E 4х + 3 = 0;х2 + 4х + 5х? - 5x - 6г) - , 20.х2 - 3x + 2х? - 7х + 12​...

Популярные вопросы