Решите неравенства: ixi больше 5 ixi больше равно 5 ixi меньше -5 ixi меньше равно 0 ixi больше -5 i2xi меньше равно 6

|x|>5    что такое модуль: |x|=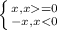

x (-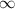;-5)(5;+).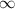

ответ: (-\infty;-5)(5;+\infty).

Аналогично с остальными:

|x|>=5

x (-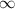<;-5][5;+).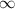

...

|x|<-5

По определению, модуль - неотрицательное число, значит х э пустое множество (перечеркнутый круг).

|x|<=0

По выше сказаному определяем, что х=0.

|x|>-5

Если |x|>=0, тогда

|x|>=0

x  (-;+).

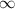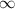|2х|<=6

x [-3;3].

ответ: [-3;3]