Решите , надо. 1)найти точки экстремума функции f(x) = x^4 - 8x^2 + 3 2)найдите наименьшее значение функции f(x) = x^3 - 6x^2 + 9 на промежутке [ -2; 2 ] . p.s. заранее .

Ответы

Зайченок157895 24.05.2020 15:46

Производная функции: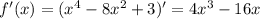 f'(x)=(x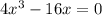^4-8x^2+3)'=4x^3-16x

f'(x) = 0; 4x^3-16x=0

4x(x^2-4)=0

Произведение равно нулю, если хотя бы один из множителей равен нулю.

$x_1=0\\ x^2-4=0~~~\Rightarrow~~~ x_{2,3}=\pm2$

___-___(-2)___+___(0)___-___(2)__+____

В точках х = -2 и х = 2 производная функции меняет знак с (-) на (+), следовательно, x=±2 - локальные минимумы.

В точке х = 0 производная функции меняет знак с (+) на (-), значит точка х = 0 имеет локальный максимум.

2) Производная функции: f'(x) = 3x² - 12x

3x² - 12x = 0

3x(x-4) = 0

x=0

x=4

Корень х=4 не принадлежит промежутку [-2;2].

Найдем теперь наименьшее значение функции на концах отрезка.

$f(-2)=(-2)^3-6\cdot(-2)^2+9=-23~~~-\min\\ f(0)=0^3-6\cdot0^2+9=9\\ f(2)=2^3-6\cdot2^2+9=-7$

ответ: $\displaystyle \min_{[-2;2]}\mathrm{f(x)=f(-2)=-23}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

КрендельЙА 05.10.2019 18:30

gandurska1 05.10.2019 18:30

nastenka082004 05.10.2019 18:30

Alena26vl 05.10.2019 18:30

daniladremov 05.10.2019 18:30

Танрпол 05.10.2019 18:30

dashoostik 05.10.2019 18:30

Alikjon 05.10.2019 18:30

Решите неравенство -3cos(1,5х+п/6) -1,5...

visor0304 05.10.2019 18:30

linabananchik 05.10.2019 18:30