РЕШИТЕ на русском: дано функция
1) решите уравнение когда
2) найдите сумму всех целых решений неравенства
, которые принадлежат промежутку [-10;10].
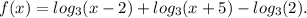
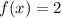
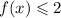

Другие вопросы по теме Алгебра
Популярные вопросы
- Что происходит с Мальцевым во время бури?...
2 - Нужно составить отзыв по рассказу Телеграмма...
1 - Накресліть графік vx(t) якщо vx=6-3t...
3 - Каково цветное решение сцены в литературном произведении и в произведении...
1 - Верны ли следующие суждения о протекании химических реакций? 1) В реакциях...
2 - Полтора километра дачник ехал на велосипеде и полкилометра шёл через лес...
1 - разобраться,только правильно...
2 - Радіус кола 4см. , а відстань від центра до прямої 3см,тоді: а) пряма перетинає...
1 - Выделите самые главные для развития действия фрагменты. Озаглавьте их....
3 - Найдите площадь фигуры, ограниченной линиями: y=-x^2-1 , y=0 , x=4 , x=1...
2
8.
1) log₃(x-2)+log₃(x+5)-log₃2 = 2
log₃((x-2)(x+5)/2) = 2
(x-2)(x+5)/2 = 3²
x²+5x-2x-10/2 = 9
x²+3x-10/2 = 9 | × 2
x²+3x-10 = 18
x²+3x-10-18 = 0
x²+3x-28 = 0
D = 3²-4×1×(-28) = 9+112 = 121 = 11²
D>0, 2 корня
x₁ = -3+11/2 = 8/2 = 4 - подходит промежутку x∈(2; +∞)
x₂ = -3-11/2 = -14/2 = -7 - не подходит он не принадлежит промежутку x∈(2; +∞)
Следовательно мы получаем что x₁ = 4.
2) log₃(x-2)+log₃(x+5)-log₃2 ≤ 2
log₃((x-2)(x+5)/2) ≤ 2
(x-2)(x+5)/2 ≤ 3²
x²+5x-2x-10/2 ≤ 9
x²+3x-10/2 ≤ 9 | × 2
x²+3x-10 ≤ 18
x²+3x-10-18 ≤ 0
x²+3x-28 ≤ 0
x²+3x-28 = 0
D = 3²-4×1×(-28) = 9+112 = 121 = 11²
D>0, 2 корня
x₁ = -3+11/2 = 8/2 = 4
x₂ = -3-11/2 = -14/2 = -7
Форма неравенства: −7≤x≤4
Запись в виде интервала: x∈[−7,4]
ответ: 1) x₁ = 4. 2) x∈[−7,4]