Решите минимуму хоть одну хоть две, очень надеюсь что

Другие вопросы по теме Алгебра
Популярные вопросы
- Колебательный контур состоит из катушки индуктивности 0,0000025гн и конденсатора...
1 - Вова, саша и коля собираю магниты. вова собрал магнитов в 2 раза больше, чем...
2 - Можно более менее точный перевод.не из переводчиков.там не понятно although modern...
3 - Сколько сантиметров составляет длина 23 метра 5 см...
3 - Подбери и запиши проверочное слово.определи,какой суффикс в данном слове.запиши...
1 - Значение температуры по шкале цельсия соответствует температуре 100 по обсалютной...
2 - Играли они прятали игрушку напиши только те предлоги и существительные которые...
2 - Укажите символ галогена : а) fe б) f в) fr г) cs...
1 - Расстояние между посёлка ми а и в 24км. из посёлка а по направлению к посылку...
2 - Какую часть литра составляет один миллилитр...
2
Упростить выражение:
Задача: Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше другого. Определить скорость каждого автомобиля.
Пусть скорость второго автомобиля — х км/ч, тогда скорость первого — х+10 км/ч. Второй был в пути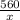 часов, а первый —
часов, а первый — 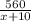 часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
часов. Зная, что второй автомобиль был в дороге дольше на 1 час, составим и решим математическую модель:
Скорость второго автомобиля — х = 70 км/ч, скорость первого — х+10 = 70+10 = 80 км/ч
скорость первого автомобиля — 80 км/ч;скорость второго автомобиля — 70 км/ч.Задача: При каких значения x функция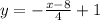 принимает положительные значения.
принимает положительные значения.
ответ: x < 12 или x ∈ (−∞; 12).