Решите квадратные уравнения
не знаю эту тему ,1 вариант
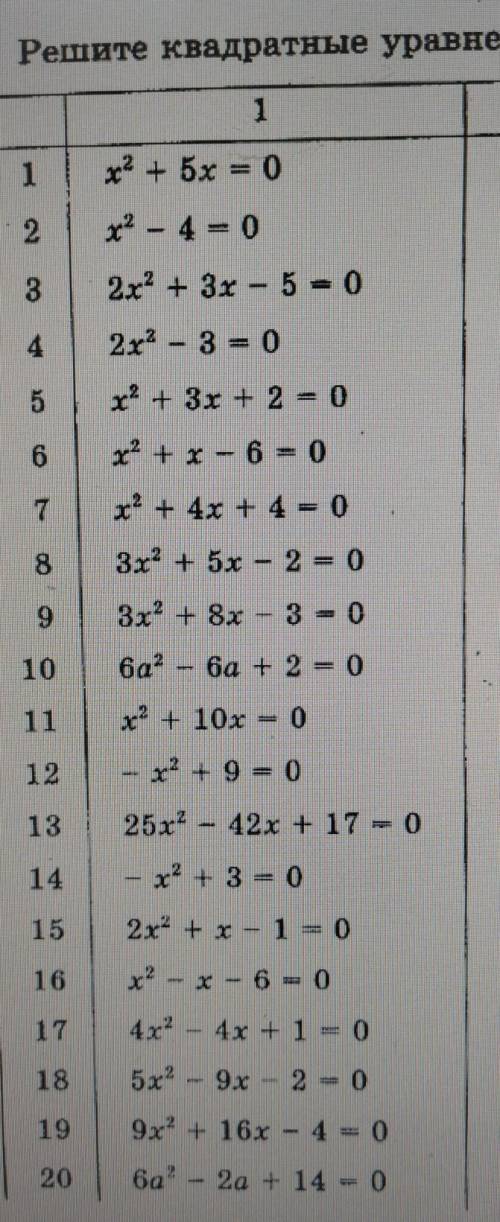
Другие вопросы по теме Алгебра
Популярные вопросы
- Расставить скобки в выражении, чтобы равенство стало верным. 60: 6+2*12=2.звездочка...
2 - (можно любой праздник в росии) prepare a short radio programme on...
2 - Составить предложение: золотистый, серебрис,гористый, лучистый,лесистый...
1 - Среднее арифметическое двух чисел равно 34,3. известно , что 2\9 одного...
1 - Из какого языка заимствовано слово сарай...
3 - По дырявому снегу плохо скользят лыжи - определить дополнение, обстоятельство...
2 - Площадь параллелограмма равно 96 см( в квадрате), нго высота равна...
2 - Скакой целью была введена кодировка unicode?...
3 - Содного участка собрали 11 центнеров 80 кг моркови что на 790 кг меньше...
2 - Вметрах 43 дм +93,2 см + 15,85 мм в сантиметрах 92 м + 93,75 см +74...
2
Объяснение:
скачай photomath он все хорошо ришает
Сначала нам нужно выразить уравнение в виде a*x^2 + b*x + c = 0, где a, b и c - это коэффициенты. В данном случае, у нас a = 1, b = -7 и c = 10. Подставим данные значения в формулу и получим следующее:
x^2 - 7x + 10 = 0
Теперь нам нужно найти корни этого уравнения. Для этого мы можем воспользоваться формулой дискриминанта:
D = b^2 - 4ac
В нашем случае, это будет:
D = (-7)^2 - 4*1*10 = 49 - 40 = 9
Теперь, когда у нас есть значение дискриминанта, мы можем продолжить и найти корни уравнения.
Есть три основных случая, которые могут возникнуть, когда мы решаем квадратное уравнение, и это:
1. Если D > 0, то уравнение имеет два различных корня.
2. Если D = 0, то уравнение имеет один корень, кратный.
3. Если D < 0, то уравнение не имеет рациональных корней.
В нашем случае, D = 9, поэтому у нас будет два различных корня. Теперь давайте воспользуемся формулой для нахождения этих корней:
x = (-b ± √D) / (2a)
Подставим данные значения:
x1 = (-(-7) + √9) / (2*1) = (7 + 3) / 2 = 10 / 2 = 5
x2 = (-(-7) - √9) / (2*1) = (7 - 3) / 2 = 4 / 2 = 2
Таким образом, у нас есть два корня: x1 = 5 и x2 = 2.
Итак, решениями данного квадратного уравнения являются x1 = 5 и x2 = 2.