1. Алгебра
  2. Решите иррационалное уравнение

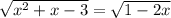
Решите иррационалное уравнение \sqrt{ {x}^{2} + x - 3 } = \sqrt{1 - 2x}
полноценное решение

BlackCat169958 BlackCat169958    3   15.12.2021 01:55    0

Ответы
olenkadergunov olenkadergunov  05.02.2022 06:49

\sqrt{ {x}^{2} + x - 3 } = \sqrt{1 - 2x} \\ { (\sqrt{ {x}^{2} + x - 3 } )}^{2} = { (\sqrt{1 - 2x} )}^{2} \\ {x}^{2} + x - 3 = 1 - 2x \\ {x}^{2} + x - 3 - 1 + 2x = 0 \\ {x}^{2} + 3x - 4 = 0 \\ d = {b}^{2} - 4ac = {3}^{2} - 4 \times 1 \times ( - 4) = 9 + 16 = 25 \\ x1 = \frac{ - b - \sqrt{d} }{2a} = \frac{ - 3 - \sqrt{25} }{2 \times 1} = \frac{ - 3 - 5}{2} = \frac{ - 8}{2} = - 4 \\ x2 = \frac{ - b + \sqrt{d} }{2a} = \frac{ - 3 + \sqrt{25} }{2 \times 1} = \frac{ - 3 + 5}{2} = \frac{ 2}{2} = 1

x = 1 не подходит по ОДЗ

ответ: x = - 4

ПОКАЗАТЬ ОТВЕТЫ
danisimokuvshn danisimokuvshn  05.02.2022 06:49

х=-4

Объяснение:

ОДЗ проверим в конце.

Возведем обе части в квадрат

Получим квадратное уравнение

x^2+3x-4=0

По теореме Виета видим два решения

х=-4 и х=1

Проверяем ОДЗ (не появились ли лишние корни после возведения в квадрат?)

Появились При х=1 подкоренные выражения отрицательны.

Х=-4 подходит.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
baburkanybekoff baburkanybekoff  05.04.2021 07:37
15. Найти площадь криволинейной трапеций y = x2, x=y2...
kisilevars2003 kisilevars2003  05.04.2021 07:37
8 А класс писал ВПР по математике. 4 человека написали на отлично, 9 на хорошо, 5 человек не сдали, остальные написали на тройки. Найдите вероятность того,что случайно...
rizakovaarina rizakovaarina  05.04.2021 07:37
Решите неравенство графическим методом Х^2-6 0Х^2-8x 0-Х^2 -2x+8 03*X^2 75-3Х^2+2х-5 02X^2 +3x+6 0​...
araydaribayaray araydaribayaray  05.04.2021 07:43
1.Расстояние между пунктами А и Б равно 260 км. Из пункта А выехал велосипедист, а через 3 ч 30 мин навстречу ему из пункта Б выехал второй велосипедист, скорость...
cariandreevac cariandreevac  24.11.2020 06:42
Функция задана формулой f(х)= -3х³ Найди: f(3)=f(-4)=​...
faa7 faa7  24.11.2020 06:42
Выбери равносильные уравнения ​...
islamkazirbaev islamkazirbaev  24.11.2020 06:42
Длина ребра 25, найти объем и площадь поверхности куба используя выражения V=a 3, S=6a 2...
wiamous1 wiamous1  24.11.2020 06:43
Функция задана формулой f (х) = -3х³ Найди f(3)=f(-4)=​...
вико2006 вико2006  30.11.2020 13:00
постройте график линейной функции игрек равен минус два икс плюс 4 с графика найдите наименьшее и наибольшее значение функции на отрезке -1 3 значение переменной...
anastasikot anastasikot  30.11.2020 13:00
Даны вершины треугольника A(−3,1),B(2,3),С(1,0) Найти уравнение высоты CD; длину высоты СD;...

Популярные вопросы