1. Алгебра
  2. Решите иррациональное

Решите иррациональное неравенство: \sqrt{x^{2} +3x - 18}\ \textgreater \ 2x+3

vikazelenaya1 vikazelenaya1    1   22.11.2019 22:55    0

Ответы
Nicalat Nicalat  10.10.2020 15:09

\sqrt{x^2+3x-18}2x+3;\ 2\sqrt{x^2+3x-18}2(2x+3);\\ \sqrt{(2x)^2+6(2x)-72}2(2x+3);\ \sqrt{(2x+3)^2-81}2(2x+3);

2x+3=t;\ \sqrt{t^2-81}2t.

ОДЗ: t^2\ge 81; |t|\ge 9; t\in (-\infty;-9]\cup [9;+\infty).

1-й случай: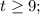 t\ge 9; в этом случае обе части неравенства положительны, и мы имеем право возводить неравенство в квадрат:

t^2-814t^2;\ 3t^2+81 Такое неравенство решений не имеет.

2-й случай: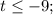 t\le -9; в этом случае левая часть неравенства неотрицательна, а правая отрицательна, поэтому неравенство выполнено автоматически. Поэтому ответом служит неравенство

t \le -9;\ 2x+3\le -9;\ 2x\le -12;\ x\le -6.

ответ: (-\infty; -6]

ПОКАЗАТЬ ОТВЕТЫ
очочов очочов  10.10.2020 15:09


Решите иррациональное неравенство: <img src=" />
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
xXDeXTeRXx xXDeXTeRXx  26.05.2020 14:06
Решить неравенство: -7x+4 -4x-11это...
Lokkinine Lokkinine  26.05.2020 14:06
и 303² решить по формуле квадрата суммы​...
сакура23 сакура23  26.05.2020 14:06
Решить систему уравнений сложения 5x+3y=-1...
ilyavladimirov1 ilyavladimirov1  26.05.2020 14:06
Розв’язати рівняння: 3х-0,1х 2 =0...
suminjenya suminjenya  26.05.2020 14:06
можно с объяснением ? напишете без улетите в бан За 3 футбольных и 2 волейбольных м мяча заплатили 544 гривен. Сколько стоит 1 футбольный и 1 волейбольная м мяч, если 2 волейбольных...
dimonnovikov0 dimonnovikov0  26.05.2020 14:06
Скоріше благаю 7 хвилииин с вираза^2b-4b^3 a^2b * 3ab^2 a^2-2ab...
Dragonhaadi Dragonhaadi  26.05.2020 14:06
у меня ща к/р у меня ща к/р​ >...
rudenkovitalik rudenkovitalik  20.11.2020 14:41
Відомо, що 2a²b⁴=9. Знайдіть значення виразу -6a²b⁴​...
дарьякозырева дарьякозырева  20.11.2020 14:41
Y=(arcsin 3x)/1-4x^2 найти производные​...
LOL8KEKYC LOL8KEKYC  20.11.2020 14:41
решите уравнения:4) c2 – 25 = c – 5.​...

Популярные вопросы