Решите дифференциальные уравнения и найдите частные решения (частные интегралы), удовлетворяющие данным условиям:
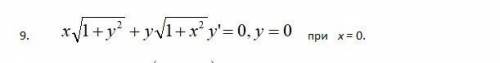
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) в кубе abcda1b1с1d1 найдите тангенс угла между плоскостями: а) abc и...
3 - Вставить пропущенные буквы. 90....
3 - 15 ! на листе бумаги проведите прямую линию, не параллельную краям листа....
2 - 1110. укажите ряд наречий.а) трижды, двое, пятерняв) вдвое, вчетвером,...
2 - Умоляю найдёт и переведите предложения в пассив...
3 - Найти в предложении фразеологический оборот: с той поры мне час от часу...
1 - Решить 12 (определите возможность взаимодействия веществ. в таблицу внесите...
1 - Толуол в отличие от бензола: 1.горит коптящим пламенем; 2.обесцвечивает...
3 - 25 положение на территории россии ладожского озера....
3 - Напишите текст про школу на мове...
1
общее решение
частное решение