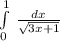
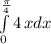
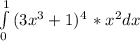
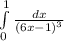
Решите что можете 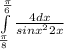[tex]\int\limits^3_0 \frac{2x}{\sqrt{16}

Объяснение:  (И-интеграл)

1) =(1/3ln|3x+1|)!(0;1)=1/3*(ln4-ln1)=1/3 ln4

2) =4x^2/2!(0;p/4)=2x^2!(0;p/4)=2(p^2 /16-0)=p^2 /8

3)     (3x^3+1)^4=81x^12+4*27x^9+6*9x^6+4*3x^3+1

  теперь это * на x^2 и получим выражение по интегралом,

=   И(0;1) (81x^14+108x^11+54x^8+12x^5+x^2)dx,  интеграл от этого выражения, равен

=(81/15*x^15+108/12*x^12+54/9*x^9+12/6*x^6+1/3*x^3)!(0;1)=

(27/5*x^15+9x^12+6x^9+2x^6+1/3x^3)! (0;1)=

27/5+9+6+2+1/3-0=17+81/15+5/15=17+86/15=17+5 11/15=22 11/15