1. Алгебра
  2. Решите -4x^2+12x-9 или=0

Решите
-4x^2+12x-9<или=0

rambobamborap08ffj rambobamborap08ffj    2   24.12.2020 00:04    0

Ответы
kolombiachka7800 kolombiachka7800  23.01.2021 00:05

-4x^2+12x -9 \leq 0

Приравняем левую часть к нулю.

-4x^2 + 12x - 9 = 0\ \ \ \ \ \Big| \cdot(-1)\\\\4x^2 - 12x + 9 = 0\\\\D = b^2 - 4ac = (-12)^2 - 4\cdot 4\cdot 9 = 144 - 144 = 0\\\\x = -\dfrac{b}{2a} = \dfrac{-(-12)}{2\cdot 4} = \dfrac{12}{8} = 1,5

-4x^2 + 12x - 9 = -4(x-1,5)^2

Посмотрим на это выражение. Квадрат любого выражения всегда будет неотрицательным числом, то есть,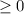 \geq 0, но оно умножится на стоящее рядом отрицательное число, из-за чего знак изменится на 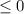\leq 0, поэтому неравенство верно при любом x.

ответ: x \in \mathbb{R}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Sk174 Sk174  22.01.2020 22:04
Нарисуйте на координатной площине xy множество точек координаты которых удовлетворяют условие: max{x^2+y^2-1,3}; min{x^2,|x|}=y...
maezsa maezsa  22.01.2020 22:00
При любом n сумма первых n членов прогрессии s_n =4(3^n - 1). найдите третий член этой прогрессии. 9 класс​...
nicgames nicgames  22.01.2020 21:57
Лодка проплыла по течению реки 3 км и по озеру 3 км.по озеру на 1 час больше, чем по течению реки. течения реки равна 4 км/ч. найдите собственную скорость лодки. ! ​...
LadyDay LadyDay  22.01.2020 21:53
Найди значение выражения: (5x−11y)⋅(5x+11y)−25x2,если x=3 и y=0,01.​...
ФамилГасанов ФамилГасанов  15.11.2019 00:48
(х-2)(х+4)×4-3(х+4)＝х(4х+1) решить уравнение​...
kamilyusupov123 kamilyusupov123  15.11.2019 01:39
Сравните x в 3 степени и x в минус 3 степени если известно что x -1 запишите свои рассуждения и точный пример​...
alinaalin2208 alinaalin2208  15.11.2019 01:30
[tex] \frac{a - b}{ {a }^{2} + ab } + \frac{a + b}{ {a}^{2} - ab } = \frac{3a - b}{ {a}^{2} - {b}^{2} } [/tex]a, b удовлетворяют равенство какое значение может принять отношение b/a?...
241cool 241cool  19.09.2019 05:50
Постройте график функции у=(3-х)(х-4) с !...
СоняЗагребова5 СоняЗагребова5  19.09.2019 05:50
Бак заполнен спиртом. оттуда отлили определённую часть спирта и заполнили бак водой. потом из бака снова вылили такое же количество смеси. в баке осталось 49 л спирта. если вместимость...
zadrotovg zadrotovg  19.09.2019 05:50
X^3+675x-(15+x)(225-15x+x^2) 0 решить неравенство...

Популярные вопросы