Решите 1 и 3 задание
Обязательно объясните каждое действие решения.
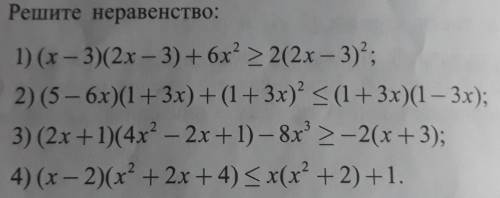
Другие вопросы по теме Алгебра
Популярные вопросы
- Вода и кисти должны быть чистыми. акварель-это краски....
2 - Если из одной стопки тетрадей переложить в другую 10 штук то тетрадей...
1 - Спростіть вираз і знайдіть його значення 2318+b+6682,якщо b=5195 829-329+m,якщо...
1 - Напрас_ное старание, прекрас_ное настроение, крепос_ная стена, извес_ный...
3 - Напишите поверхность земного шара .острова моря и т.д.только не отсебятину...
1 - Напишите краткий перессказ про царевну-лягушку...
1 - Вітаміни коштують 57,35 подоржачалина 8 %.яка нова ціна вітамінів...
1 - Сообщение про одного героя отечественной войны 1812 года....
3 - Проверочные слова к словам старшина косьба торгаш окольцевать возобновить...
2 - Найди: 5/20 от 645 260 и 3/9 от 26 712...
2
1) (x-3)(2x-3)+6x² ≥ 2(2x-3)²
Нужно раскрыть скобки2x²-3x-6x+9+6x² ≥ 2(4x²-12x+9)
Если нужно повторяем это действие2x²-3x-6x+9+6x² ≥ 8x²-24x+18
Приводим подобные слагаемые(они подчеркнуты)8х²-9х+9 ≥ 8x²-24x+18
Убираем равные слагаемые(они подчеркнуты)-9х+9 ≥ -24x+18
Переносим х и числа в разные стороны-9х+24x ≥ 18-9
Вычисляем15х ≥ 9
Получаем дробь(х ≥х ≥ или х ≥ 0.6
или х ≥ 0.6
3) (2х+1)(4х²-2х+1)-8х³≥-2(х+3)
Нужно раскрыть все скобки ((2х+1)(4х²-2х+1) можно упростить используя формулу (a+b)(a²-ab+b²)=a³+b³)8х³+1³-8х³ ≥ -2х-6
Сокращаем противоположные слагаемые(они подчеркнуты)1³ ≥ -2х-6
Переносим х и числа в разные стороны2х ≥ -6 - 1³
Вычисляем2х ≥ -7
Получаем дробь (х ≥х ≥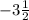 или х ≥ -3.5
или х ≥ -3.5