1. Алгебра
  2. Решите, 1. х+6 х-6 - х+1 х-1

Решите, 1. х+6 х-6 - х+1 х-1 2. при каких натуральных n дробь 7n2+4n+12 принимает натуральные значения? n 10

PFAN PFAN    1   29.09.2019 01:50    0

Ответы
Даша46111 Даша46111  09.10.2020 01:46

1)~\dfrac{x+6}{x+1}-\dfrac{x-6}{x-1}=0\medskip\\\dfrac{\left(x+6\right)\left(x-1\right)-\left(x-6\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=0\medskip\\\dfrac{x^2+5x-6-x^2+5x+6}{x^2-1}=0\medskip\\\dfrac{10x}{x^2-1}=0\medskip\\\begin{cases}x=0\\x\neq\pm1\end{cases}\Leftrightarrow x=0

2)~\dfrac{7n^2+4n+12}{n}=7n+4+\dfrac{12}{n}

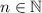Очевидным образом, к первому слагаемому не прилагается никаких ограничений. А вот к последнему, в первую очередь, n\neq 0, но ноль нам не попадется т.к. ищем n\in\mathbb{N}. Нетрудно догадаться, что нужны n\leqslant 12, причём такие, что будут делить 12.

Получаем - n\in\left\{1;~2;~3;~4;~6;~12\right\}\subset\mathbb{N}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
inakenyakakyevich inakenyakakyevich  10.09.2020 01:18
Знайдіть похідну функції, повне розв язання ​...
gilkin01 gilkin01  10.09.2020 01:17
Решите неравенство |x²-5x| меньше или равно x...
ник4858 ник4858  13.06.2019 07:00
Постройте график с таблицей поже y=3/х ,y=18/х...
ksskjskdjdkdk ksskjskdjdkdk  13.06.2019 07:00
Корень из x^2+2х+10 =2х-1 решите .....
EvaMilka EvaMilka  13.06.2019 07:10
Найдите наибольшее целое число,пренадлижашее числовому промежутку [-18; -6,7)...
anhelinayeremenko30 anhelinayeremenko30  05.07.2019 00:10
Найдите значения числового выражения 9,4-8,2+0,6-2,8...
ReutovTema222 ReutovTema222  05.07.2019 00:10
Прочитайте выражение,назовите основание и показатель степени: 1)9в6 степени 2)2,4в7 степени 3)0,3в5 степени )в2 степени ,6)в3 степени )в 11 степени 7)73в 1 степени 8)(3р)в...
денис20062002 денис20062002  05.05.2020 09:59
А) х 2 + 5х + 4 = 0 б) у 2 – 9у + 20 = 0 РЕШИТЕ САМОСТОЯТЕЛЬНА ИДЕТ...
Elenka9272 Elenka9272  05.05.2020 09:59
1)18a-3a²18a²-48a2)8p-4015-3p3)4-x²10-5x​...
djdhd1 djdhd1  05.05.2020 09:59
На изготовление 425 деталей первый рабочий затрачивает на 8 часов меньше, чем второй рабочий на изготовление 525 таких же деталей. Известно, что первый рабочий за час делает...

Популярные вопросы