решить x-4/x+19+x-19/x+4=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Вмагазине было 60 кг сахара. до обеда продали одну треть этого сахара, а после...
1 - Почему хлеб это существительное полный ответ ну потому помню...
3 - Склади речення за питаннями.який? хто? що робить? що? хто? де?...
1 - Какие растения используют в строительстве...
3 - Подготовьте краткое сообщение о простейших-паразитах. составьте план сообщения,...
2 - Напишите, почему вы смотрите телевизор и почему нет.(tv advantages- 5 примеров,...
3 - Люди ! описание буратино я давно читал и не помню . заранее...
2 - Маше купили аквариум с рыбками. ещё у маши была кошка тася. кошке тасе нравились...
3 - Какие формы числа имеют слова работа, ворота, прятки, краснота, помидоры?...
1 - Нужно отзыв по повести записки маленькой гимназистки...
3
x = ±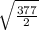
Объяснение:
думаю задание звучало так
ОДЗ: x ≠ -19; x ≠ -4.
2x²- 361 - 16 = 0
2x² = 377
x = ±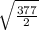
------------------------
или так
x-4/x+19+x-19/x+4 = 0
ОДЗ: x ≠ 0
x²-4 +19x + x² -19 +4x = 0
2x² + 23x -23 = 0
D = 23*23 - 4 * 2 * (-23) = 23 * (23 + 8) = 23*30 +23 = 690 + 23 = 713
x1 = (-23 -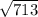 )/4
)/4
x1 = (-23 +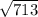 )/4
)/4