Решить вариант 4 1.вычислите: a)3^-5-3; б)(1/5)^-2-5; в) (7^-3)^2-49^3/7. 2 найдите значение выражения: а) 1/8 ^6√64-2 ^3√-125+√1; б) √121-0,01; в) √343/√7; г)(^5√3)^-10. 3.решите уравнение: а) х^2=13; б) 32х^5=1; в) х^6=-16; г) -8-х^3=0.
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему великий энштейн сказал о музыке иогана себастьяна баха:...
1 - Решите дробь. х^2-16- числитель 3ху- знаменатель. умножить на 6у-...
3 - По информатике , сравните хранение файлов в компьюторе и книг в...
3 - Натуральные числа m, n таковы, что нод(m,n)+нок(m,n)=m+n...
2 - Чай пить не дрова рубить. без тире?...
3 - Определите атмосферное давление на вершине горы если у её подножия...
2 - Реши примеры используя результат первого примера а)4*25= б) 6*15=...
3 - Раздел ii. причастие вариант 3 часть 1 к каждому 1—20 даны четыре...
3 - Чему равно делимое, если делитель равен 17, неполное частное 11...
2 - Как можно спеть песню антошка в другом стиле...
1
1. a)
б)
в)
2. а)
б)
в)
г)
3. а)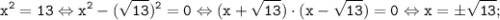
б)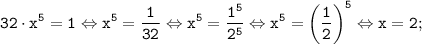
в)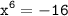 , так как x⁶≥0 и -16<0, то уравнение не имеет решений;
, так как x⁶≥0 и -16<0, то уравнение не имеет решений;
г)