Решить в целых числах уравнение: 3x+y=37/(x2+1) .
Другие вопросы по теме Алгебра
Популярные вопросы
- В электрическом чайнике мощностью 2000 Вт можно за 8 минут вскипятить 1,5 литра...
1 - , краткий,ясный,полный и правильный ответ....
3 - с заданием (если не сложно, не могли бы вы ещё и объяснить)...
2 - 4. Упростите выражение (-x-7y)^2 - (х + 7 уX7y-x) А) 2x2 + 14B) 2x2 - 14С) х2...
1 - Какой жанр у (Щелкунчик) Чайковский...
2 - Назови виды данной величины. Количество бактерий. Рассеянная Качественная Непрерывная...
2 - Эссе жазасыңдар. Тақырыбы: Сатқындықтың жазасы - өлім 200 слов Ұлының жасаған...
1 - 3 Match 1-5 with a-h. There are three letters you do not need to use. 1 You...
2 - Вставить пропущенные глагол и окончание : 8) Сенің шешең театрға бар ма? 9)...
3 - График прямой пропорциональности проходит через точки а) А(-6;2) б) А(3;6) в)...
2
3x+y - целое => 37 делится нацело на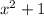 . Т.к. 37 - простое, то
. Т.к. 37 - простое, то 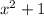 может принимать одно из значений
может принимать одно из значений 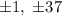 .
. 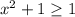 => остаются варианты 1 и 37
=> остаются варианты 1 и 37
ответ: (0;37), (6;-17), (-6;19)