Решить уравнения: 1) sinx - cos2x + 1 = 0 2) sin2x = 4sin(в квадрате)x
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите заряд, создающий электрическое поле, если на расстоянии 5 см от заряда...
3 - В технике напряженность электрических полей не превышает Е= 107 Н/Кл. Сравните...
3 - Какова напряженность электрического поля на расстоянии 1 м от точечного заряда...
3 - Два одинаковых маленьких заряженных шарика, подвешенные на нитях одинаковой длины,...
1 - Два крошечных металлических шарика массой по 10 мг, имеющие заряды, подвешены...
3 - Шарик массой 150 мг, подвешенный на тонкой непроводящей нити, имеет заряд 10 нКл....
1 - Железная балка наглухо заделана между двумя стенами при температуре 0 °С. Какое...
1 - На каком расстоянии от шарика А (рис. 113), погруженного в керосин, должна быть...
3 - На изолированной подставке расположен вертикально тонкий фарфоровый стержень,...
2 - Докажите, что если два одинаковых металлических шарика, заряженные одноименно...
2
1) sinx - cos2x + 1 = 0
sinx - cos²x + sin²x + cos²x + sin²x = 0
2sin²x + sinx = 0
sinx (2sinx + 1) = 0
a) sinx = 0
x₁ = πn
b) 2sinx + 1= 0
2sinx = -1
sinx = -0.5
x₂ =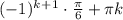
2) sin2x = 4sin²x
2sin x·cos x - 4sin²x = 0
2sin x · (cos x - 2sin x) = 0
a) sinx = 0
x₁ = πn
b) cos x - 2sin x = 0
делим на cos x
1 - 2tg x = 0
tg x = 0,5
х₂ =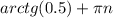
1) sinx - cos2x + 1 = 0
1) sinx - 1+2sin^2x + 1 = 0
2sin^2x+sinx=0
sinx(2sinx+1)=0
sinx=0 -> x=pi*k
2sinx=1 -> x=(-1)^n * pi/6 + pi*n
2) sin2x = 4sin^2x
2sinx*cosx-4sin^2x=0
2sinx(cosx-2sinx)=0
a)2sinx=0 -> x=pi*k
б)cosx-2sinx=0 делим на кореньиз 5
1/√5cosx - 2/√5 sinx=0
sin(arcsin 1/√5 - x) =0
arcsin 1/√5 - x = pi*n -> x=arcsin 1/√5 - pi*n