Решить уравнение.
За неправильный ответ в бан.
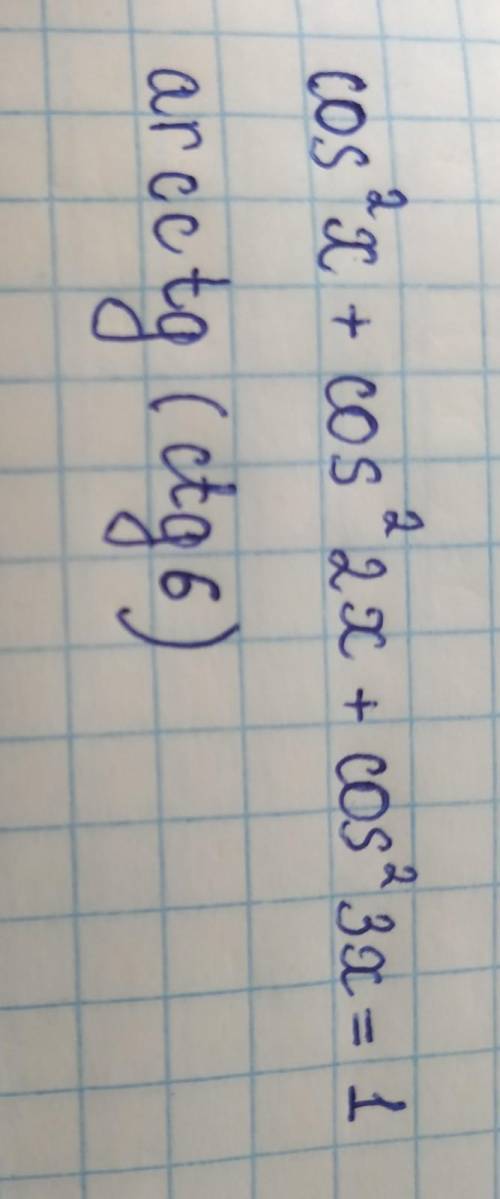
Другие вопросы по теме Алгебра
Популярные вопросы
- 3) в чем новаторство любовной лирики пушкина? назовите ее черты4) какому периоду...
2 - Написать сочинение «почему я не хочу в деревню» минимум 100 слов,заранее...
2 - Годовая программа выпуска продукции предприятия 10 000 шт. изделий. годовой расход...
3 - 7. какие из реакций пройдут до конца: а) kbr + i2 -б) ki + cl2 -в) kcl + br2-г)...
1 - Найти производную функции 1)f(x)=(2/x+3x)(кореньx-1) 2)f(x)=1/3sin^3 x(6cos^2 x+7)...
1 - Нужно найти координат вектора ав и длину вектора ав...
3 - Нпзввть приклад гіпербуди та пояснить з яеою метою леся українка їх використовувала...
2 - Швидкість тіла при рівномірному русі можно визначити за формулою : a)v=st б)v=s/t...
2 - 96. яку траєкторію під час руху по прямолінійнійдорозі описує центр колеса автомобіля?...
1 - Ть з тестами з 7 по 10. тобто всі ці...
2
Множество решений уравнения а) является подмножеством множества решений уравнения б), поэтому в ответ можно записать только решения б) и с) .
ответ: