1. Алгебра
  2. Решить уравнение z^2-(6+i)z+10+6i=0

Решить уравнение
z^2-(6+i)z+10+6i=0

777кошка777 777кошка777    3   08.02.2022 12:45    0

Ответы
vika2087 vika2087  08.02.2022 12:50

z^2-(6+i)z+10+6i=0

D=(6+i)^2-4(10+6i)=

=36+12i+i^2-40-24i=i^2-12i-4=-5-12i

Необходимо извлечь корень из числа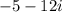 -5-12i. Для этого обозначим искомое значение.

Пусть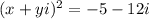 (x+yi)^2=-5-12i.

x^2+2xyi+y^2i^2=-5-12i

x^2-y^2+2xyi=-5-12i

Два комплексных числа равны когда равных их действительные и мнимые части:

\begin{cases} x^2-y^2=-5\\ 2xy=-12 \end{cases}

Из второго уравнения выразим:

y=-\dfrac{6}{x}

После подстановки в первое уравнение получим:

x^2-\left(-\dfrac{6}{x}\right)^2=-5

x^2-\dfrac{36}{x^2}=-5

x^4+5x^2-36=0

Решаем биквадратное уравнение:

D=5^2-4\cdot1\cdot(-36)=169

x^2\neq \dfrac{-5-\sqrt{169} }{2} =-9

x^2=\dfrac{-5+\sqrt{169} }{2} =4

\Rightarrow x_1=2\Rightarrow y_1=-\dfrac{6}{2} =-3

\Rightarrow x_2=-2\Rightarrow y_2=-\dfrac{6}{-2} =3

Таким образом, искомый корень из дискриминанта исходного уравнения:

x+yi=\pm(2-3i)

Решения исходного уравнения:

z=\dfrac{6+i\pm(2-3i)}{2}

z_1=\dfrac{6+i+2-3i}{2} =\dfrac{8-2i}{2} =4-i

z_2=\dfrac{6+i-2+3i}{2} =\dfrac{4+4i}{2} =2+2i

ответ: 4-i; 2+2i

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
MMMOZG MMMOZG  13.04.2020 14:01
Писать долго поэтому скидываю фото! Нужна в решении...
mashapermyakova mashapermyakova  13.04.2020 14:02
решить неравенства с графика ​...
Alyona2022 Alyona2022  13.04.2020 14:02
Является ли последовательность (аn) арифметической прогрессией, если она задана формулой n-го члена:1) аn= 6+7n2) an= 2n-1/53) an= 1/n + 2В случае утвердительного ответа укажите a1...
Dima1Tap Dima1Tap  13.04.2020 14:02
4.Скільки коробок двох розмірів потрібно мати, щоброзкласти в них 100 Олівців, якщо в одні коробкиможна положити по 4 олівці, а в інші — по 15 Олівців?​...
Не007 Не007  13.04.2020 14:02
Напиши уравнение касательной к графику функции y=4x в точке x=0,5.ответ:​...
НеПøтêpяHHåя НеПøтêpяHHåя  13.04.2020 14:02
При каких значениях x двучлен 8x−12 принимает отрицательные значения? (В первое окошко введи соответствующий знак: « » или « ».) ответ: при x...
dariarez dariarez  13.04.2020 14:02
Вычислите значение тригонометрических функций если 1) sin = - 5/13 и 3/2 ? 2) cos = - 8/18 и /2 ? 3) tg =8/15 и...
LutsenkoRodion LutsenkoRodion  20.01.2020 08:47
Вынеси общий множитель за скобки: 3,9g+1,3p+7,8 ответ: ⋅ ( g p + )...
daniilsemkin05 daniilsemkin05  20.01.2020 08:43
1. изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию: а) x /=4 б) 0=y=5...
zwitterlord2 zwitterlord2  20.01.2020 08:42
Найди значение выражения 2,63m−2,63n, если m=110,n=10. !...

Популярные вопросы