Решить уравнение x в степени 6 - 5х в степени 3 +4=0 решить неравенство 2*х в степени 2- х -3 > = 0 построить график и исследовать у=cos x -1 и y=1(x+2)-2

Ответы

Katerina3069 08.09.2020 21:21

X⁶-5x³+4=0
x³=t
t²-5t+4=0
t₁+t₂=5 (-за теормою Виета)
t₁*t₂=4
t₁=4
t₂=1

х³=t
x=∛t
x₁=∛4
x₁≈1.5874
x₂=∛1
x₂=1

x=∛4 и х=1

2*х²- х -3≥ 0
$D=(-1)^2-4*2*(-3)=1+24=25 \\ 
x_1= \frac{-(-1)- \sqrt{25} }{2*2} = \frac{1-5}{4}= \frac{-4}{4} =-1 \\ x_2= \frac{-(-1)+ \sqrt{25} }{2*2} = \frac{1+5}{4}= \frac{6}{4} = 1.5$

__+____-1____-___1.5____+______>x

x∈(-∞; -1]∪[1.5; +∞)

y=cosx-1
а) Область определения: D (cos x-1) = R .
б) Множество значений: E (cos x-1 ) = [ – 2 , 0]

в) Четность, нечетность: функция четная.

г) Периодичность: функция периодическая с основным периодом T = 2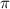 $\pi$

Точки пересечения с осямии:
ОХ:
cos x -1= 0
cos x =1
$x=2 \pi n,~~~n\in Z$
OY:
cos(0)-1=1-1=0

Промежутки знакопостоянства.:

cosx-1>0

сosx>1 - не существует, поэтому функция лежит ниже оси ОХ

интервалы возрастания и убывания:

y'=(cosx-1)'= (cosx)'-1'= -sinx

функция возрастает:

-sinx>0

$x \in (2 \pi n-\pi n~~~;~~ \pi ),~~~~n \in Z$

функция убывает:

-sinx<0

$x \in (2 \pi n~~~;~~ \pi n + \pi),~~~~n \in Z$

Экстремумы:
(-sinx)'= -cosx
-cos(0)=-1
-1<0 значит точка x = 0 точка максимума функции
Решить уравнение x в степени 6 - 5х в степени 3 +4=0 решить неравенство 2*х в степени 2- х -3 > =