Алгебра: Решить уравнение в целых числах 4ab+4bc+4ac=5abc+14

ответ: Все перестановки (1;5;6) , (1;2;3)Объяснение:Поскольку левая часть делится на 4, то и правая часть делится на 4.Число 14- четное, но тогда и число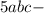 четноеТо есть среди чисел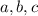 - хотя бы одно четное. Пусть произвольно, в силу симметрии задачи: Левая часть остается четной, а значит и правая часть должна быть четной, но поскольку 7- нечетное число, то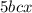 - тоже нечетное число, а значит все числа 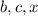- нечетные. Предположим, что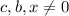 Поделим обе части равенства на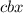 Предположим, что одновременно верно, что :`Но...

Решить уравнение в целых числах 4ab+4bc+4ac=5abc+14

Ответы

mumuminecraft 15.10.2020 16:00

ответ: Все перестановки (1;5;6) , (1;2;3)

Объяснение:

4ab+4bc+4ac=5abc+14

Поскольку левая часть делится на 4, то и правая часть делится на 4.

Число 14- четное, но тогда и число 5abc- четное

То есть среди чисел a,b,c - хотя бы одно четное. Пусть произвольно, в силу симметрии задачи:

a=2x

$8bx +4bc+8cx = 10bcx +14\\4bx +2bc+4cx = 5bcx +7\\$

Левая часть остается четной, а значит и правая часть должна быть четной, но поскольку 7- нечетное число, то 5bcx - тоже нечетное число, а значит все числа b,c,x - нечетные.

Предположим, что $c,b,x \neq 0$

Поделим обе части равенства на cbx

$\frac{4}{c} +\frac{2}{x} +\frac{4}{b}- \frac{7}{cbx} = 5$

Предположим, что одновременно верно, что :`

$|c|1\\|b|1\\|x|1$

Но тогда, в силу того, что все числа целые, а так-же того, что какой бы знак не имели числа x,b,c, всегда хотя бы одно из выражений :

4/c; 2/x ; 4/b ; -7/cbx - отрицательно.

Действительно, если окажется, что -7/сbx > 0 , то хотя бы одно из чисел с,b,x меньше нуля.

$\frac{4}{c} +\frac{2}{x} +\frac{4}{b}- \frac{7}{cbx} \leq \frac{4}{2} +\frac{2}{2} +\frac{4}{2}- \frac{7}{8} = 5- \frac{7}{8} < 5$

Поскольку, число 7/8 - cамое маленькое среди данных 4-x чисел.

То есть мы пришли к противоречию, а значит, хотя бы одно из чисел, a,b,x равно +-1. Тогда в силу симметрии задачи, в уравнении

4ab+4bc+4ac=5abc+14

одно из чисел a,b,c равно либо +-1 либо +-2.

1) a=1

$4b+4bc+4c=5bc+14\\4b+4c-bc = 14\\4b +c(4-b) = 14\\4b-16 +c(4-b) =-2\\ -4(4-b) +c(4-b) = -2\\ (c-4)(b-4) = 2\\ \left \{ {{c-4=+-2;+-1} \atop {b-4=+-1;+-2}} \right. \\$

$c_{1} =6\\b_{1} =5$

$c_{2} =5\\b_{2} =6$

$c_{3} =2\\b_{3} =3$

$c_{4} =3\\b_{4} =2$

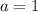
В силу симметрии задачи, все перестановки чисел 1,2,3 и 1,5,6 являются решениями системы.

2) a=-1

$-4b +4bc -4c = -5bc +14\\-4b-4c+9bc = 14\\4b+4c-9bc = -14\\4b +c(4-9b) = -14\\36b+9c(4-9b)= -126\\36b-9c(9b-4) =-126\\36b-16 -9c(9b-4) = -142\\4(9b-4) - 9c(9b-4) = -142\\(9c-4)(9b-4) = 142\\142=2*71\\9c-4= 71\\9c=75 - netreshenij\\9c-4=-71\\9c=-67 - netreshenij$

В других случаях из симметрии так же нет решений.

3) a=2

$8b +4bc +8c = 10bc+14\\4b+2bc+4c =5bc+7\\4b-3bc+4c = 7 \\4b - c(3b-4) = 7\\12b-3c(3b-4)=21\\12b -16 -3c(3b-4) = 5\\(3b-4)(3c-4)=-5\\3b-4=5\\b=3 - etot sluchai yzhe bil\\3b-4=1\\3b=5 - net reshenij\\$

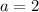
В других случаях так же нет решений.

4) a=-2

$-8b +4bc-8c = -10bc+14\\-4b+2bc-4c = -5bc +14\\-4b + 7bc -4c = 14\\-4b +c(7b-4) = 14\\-28b+7c(7b-4) = 98\\-28b +16 +7c(7b-4) = 114\\(7c-4)(7b-4) = 114 \\7c-4 = +-57\\7c = 61 - net reshenij\\7c=-53 -net reshenij\\$

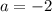
Таким образом больше решений нет.

Осталось рассмотреть: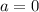 a=0

4bc=14

Решений нет.

Примечание: можно было получить разложение сразу для произвольного a, а потом просто подставлять в него различные a. Так было бы немного быстрее и компактнее.

(4a+4c-5ac)(4a+4b-5ab) = 16a^2-70a+56