Решить уравнение тригонометрическое
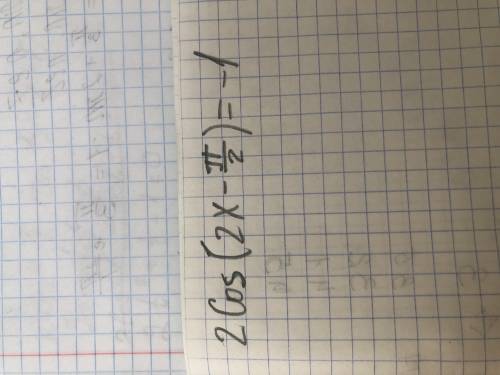
Другие вопросы по теме Алгебра
Популярные вопросы
- определить какие из данных углов тупые Какие острые если известны их величины....
3 - Порівняйте образ ромео напочатку й наприкінці твору...
3 - Закончить уравнение реакции, уравнять, записать полное и сокращение ионное уравнения:...
1 - Очень Как Стендаль показывает эволюцию, деградацию героя, или что другое - по...
3 - Спишіть речення, розставляючи пропущені розділові знаки. визначте кількість...
2 - Распредели в 2столбика: электризация тела возможнаэлектризация тела невозможна1....
2 - Двигаясь в электрическом поле протон перешел из одной точки в другую, потенциал...
3 - Напишите в тетради эссе о церковной реформе Петра1 цели и задачи которые онв...
3 - Який зміст метафор моя любов – рожевий кіт і моя любов – веселий спів ...
1 - Почему главный герой рассказа И.А.Бунина Подснежник очень ждал отца и расстраивался...
3
ответ: x = (- 1 )ⁿ⁺¹• π/12 + πn/2 , nЄ Z .
Объяснение:
2cos( 2x -π/2 ) = - 1 ;
2cos( π/2 - 2x ) = - 1 ; ( функція у = соsx - парна )
cos( π/2 - 2x ) = - 1/2 ;
sin2x = - 1/2 ;
2x = (- 1 )ⁿarcsin(- 1/2 ) + πn ; nЄ Z ;
2x = (- 1 )ⁿ⁺¹arcsin( 1/2 ) + πn ;
2x = (- 1 )ⁿ⁺¹• π/6 + πn ;
x = (- 1 )ⁿ⁺¹• π/12 + πn/2 , nЄ Z .