Решить уравнение sin2x+sinxcosx-3cos2x=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить план-пересказ по одному предложению к каждой картинке....
3 - Складіть словосполучення із прикметниками та введіть їх у речення із словами:...
1 - Уривнобичну трапецию, перыметер якои доривнюе 14 см впысано коло. знайдить довжыну...
2 - Как изменилась разница между зональными временем волгограда и солнечным временем...
3 - Запишите переодическую дробь в виде обыкновенной 0,(7) 2,4(3)...
1 - Диолог, вставить недостающие слова...
2 - Дано: ао=до; ов=ос.довести: ∆аов=∆дос...
2 - 3. укажіть речовини, які реагують з етиленом: а) бромна вода; в) хлор ( при...
2 - Известно что цветение воды наносит вред обитателям водоемов однако сами цианобактерии...
1 - Як зміниться відстань між свічкою та її зображенням у плоскому зеркалі ,якщо...
1
Разделим левую и правую часть уравнения на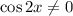 :
: