Решить уравнение sin2x-cosx=0 и выбрать корни, которые принадлежат промежутку (-п/2;п)
Ответы
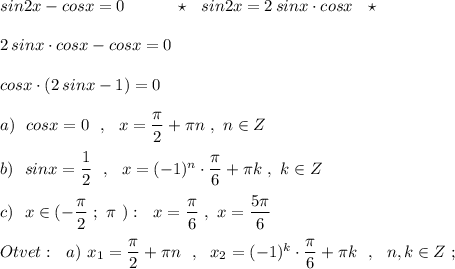
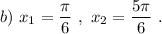
Другие вопросы по теме Алгебра
Популярные вопросы
- С! ) (1)complete these sentences in the past simple.1 his mother_(hear) a loud...
2 - План до казки полліанна 12 розділ будласка дуже треба...
3 - Найдите частное числе 25/42 и 5/7 вычислите 3/4 : 5/11...
3 - Природні зони вологих екваторіальних лісів (сельвас) *який грунт? * який клімат?...
3 - График функции y=-x^2+4x+5 какие из следующих утверждений неверны1)f(3)=82)f(x)...
3 - Укажи, с какой выталкивающей силой действует пропан на тело объёмом 1м³ при 0°с...
2 - 30 х 2, 9 - 2, 9 x 28 + 28 x 2, 7- 2, 7 x 26+ 26 x 2, 5 - 2, 5 x 24 + 24 x 2,...
1 - Как называется мемориальный комплекс...
1 - Если край каждой ячейки, показанной на рисунке, составляет 2 см найти общую цифру...
3 - Лиханов альберт - последние холода о чём это рассказ, чем закончился ?...
1