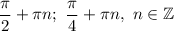Решить уравнение: sin2x=√2|cosx|
Другие вопросы по теме Алгебра
Популярные вопросы
- Мотоцикл, трогаясь с места, движется с ускорение 3м/с^2. какую скорость приобретёт...
3 - Соединениями с ковалентно неполярной и ковалентно полярной связью является соответствено:...
1 - Нужно само решение к если вороны сядут по одной на каждую березу, то не хватит одной...
2 - Написать сказочную о дикорастущем или...
3 - 1: что такое отзыв (ударение на о)и отзыв (ударение на ы)2: что такое пикировать...
3 - Что значит цитата у солнца есть один недостаток: оно не может видеть самого себя....
1 - 1)имеется сталь двух сортов с содержанием никеля в 5% и 40%.сколько нужно взять...
2 - Продолжи каждое предложение так, чтобы получилось сложное предложение и простое...
2 - Іть скласти діалог листочків берізки та клена.на завтра.дуже треба. наперед...
2 - 6класс какой город расположен выше дели или пекин, мехико или бразилиа? (учебник-...
2
1. Раскроем модуль при условии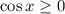 :
:
Однако корни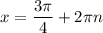 не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:
не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:
2. Раскроем модуль при условии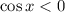 :
:
Заметим, что первое уравнение не удовлетворят условию раскрытия модуля. Продолжаем решать только второе уравнение:
Однако корни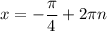 не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:
не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:
3. Объединим решения, полученные в предыдущих пунктах:
Или более кратко:
ответ: