Решить уравнение разложением на множители cos7x-cosx-sin4x=0
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Как найти синус (косинус, тангенс, котангенс) данного угла. 2. Как найти угол,...
1 - В теплоизолированном сосуде находилось v1 = 5 моль неона с температурой t1 = 0...
3 - Правление Павла I . Задание No1.1. Сколько лет продлилось правление Павла і?2....
2 - 11-тапсырма. Мәтіндегі күрделі сөздерді теріп жаз. Олардыңмағынасын айт....
3 - Характеристика Антипка и наталки ,цикави Географични назвы из твору....
1 - Периметр треугольника равен 35 см. Сторона АВ на 3 см больше стороны ВС, а сторона...
3 - Скласти 2 односкладних речень про весну, і два двоскладних речень про весну ...
2 - ІТЬ БУДЬ ЛАСКА 4 і 6))БУДУ ДУЖЕ ВДЯЧНАА :з...
2 - 1.Какой участок земной коры лежит в основании В-Е равнины? А. Сибирская платформа...
3 - Найдите точку пересечения прямых игрек минус икс равен 1 и 2 Икс плюс игрек равен...
2
Решить уравнение разложением на множители cos7x-cosx-sin4x=0
Объяснение:
cos7x-cosx-sin4x=0
1)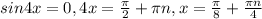 ,n∈N
,n∈N
и
2)
ответ.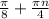 ,
,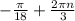 ,
,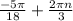 ,n∈N.
,n∈N.