Популярные вопросы
- X-8/x+2=7/3 решите уравнение...
1 - 1. Вычисли, записывая примеры в столбик. 456 + 196 164 • 5 720...
2 - Под воздействием бактерий происходит превращение листьев и древесины,...
3 - Чотирикутники AMNK і BCDL подібні AM/BC =7. Чому дорівнює відношення:...
1 - Кінці діаметра віддалені від дотичної до кола на 2,8 м и 1,2...
3 - Почему+наше+государство+уделяет+большое+внимание+семье+особенно+детям...
1 - решит к.р по Английскому языку 9 класс. 1. Complete the sentences...
1 - С плотины высотой 10 м за 10 мин падает 200 т воды. Какая мощность...
2 - Виконайте роботу на бланку для домашніх завдань. Завдання 1....
1 - 10 прикладів алегорії до характеристики коня Шептала в...
3
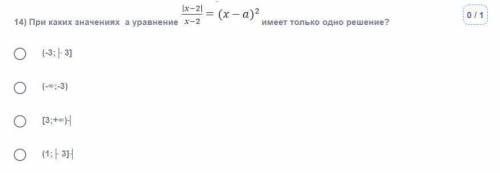
Если x-2 < 0 ,т. е x < 2
|x-2|=-(x-2)
поэтому уравнение принимает вид:
Если x-2 >0 ,т. е x > 2
|x-2|=x-2
поэтому уравнение принимает вид:
Чтобы выполнялось требование задачи, один из найденных корней не должен удовлетворять условию x > 2
Так как
то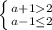
О т в е т. 4) (1; 3]