Решить уравнение. ответ x = 1, но обосновать ни аналитически, ни графически у меня не вышло 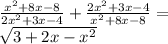
Другие вопросы по теме Алгебра
Популярные вопросы
- Из города а в город в выехал автомобиль со скоростью 60 км/ч. водитель...
3 - Сократите дробь: 4a2+12a+9\2a2+a-3 !...
2 - (a+7)²+2(a+7)(a+3)+(a+3)² при a= -6,5 и решить выражение...
1 - Реши систему уравнений методом подстановки.{4−5(0,2m−2x)=3(3x+2)+2m{4(x−4m)−(2x+m)=3−2(2x+m)...
3 - Прочитайте эпизод спор дитей о дороге из сказки м. м. пришвина...
1 - Впредложениях отметьте существительные 2-ого склонения 11.дым от...
2 - Что такое ум vii 7 в сольфеджио и его разрешения...
2 - Написать психологический портрет про себя по этим четырём надо!...
2 - На рис.128 изображены лучи, на зеркало. постройте отраженные лучи,...
1 - Практична робота з фізики 11 клас на тему: вивчення треків заряджених...
2
х=1
Объяснение:
обозначим образно в левой части уравнения дроби а и 1/а соответственно.
используем свойство неравенства коши:
среднее арифметическое ≥ среднего геометрического, →
среднее арифметическое:
(а + 1/а) /2
среднее геометрическое:
²√(а*(1/а)) = √(а/а) = √1 =1
то есть (а + 1/а)/2≥1
или а + 1/а≥2
учитывая введённые обозначения получаем, что левая часть исходного уравнения ≥2,
соответственно правая часть исходного уравнения также должна быть ≥2:
√(3+2х-х²)≥2
или
3+2х-х²≥4
0≥4-3-2х+х²
х²-2х+1≤0
(х-1)²≤0
так как (х-1)²≥0 при любом х, то (х-1)²≤0 имеет решение лишь при х-1=0 или х=1
подставив х в исходное уравнение убеждаемся, что данное решение принадлежит одз и действительно является решением (если бы не подошло, то уравнение не имело бы решений)