Решить уравнение: (6-y) ^2 y^2 + (6-y) y = 72 желательно написать решение. заранее всем !
Другие вопросы по теме Алгебра
Популярные вопросы
- Расстояние между пристанями а и в на реке плот проплывает за 15...
3 - Что значит уметь любить по рассказу юшка...
2 - 1)сторона квадрата равна 7,3см.найдите площадь квадрата.2)ребро...
1 - Сочинение-рассуждение что чувствуют собаки а.и....
3 - Современником царя алексея михайловича не является а)степан разин...
3 - Осевые и центральная симметрии правило...
3 - Строение зелёных клеток листа мха сфагнума...
3 - Найдите не определённую форму глагола и выпишите. -салауатты өмір...
3 - Рссказ полковник на и после . вот тема сочинения почему рассказ...
2 - Жесткие прямые волосы широкое лицо и узкая глазная щель. это признаки?...
3
ответ: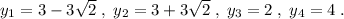
Объяснение: