Решить уравнение : (4x -8) · 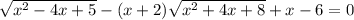
Популярные вопросы
- Предложения из has gone to...
3 - Масу тіла 200 г виразити в тонах у стандартному вигляді. 1) 2.10(-2)т 2) 2.10(-4)...
2 - Сделать ментальную карту на образ Гринёва...
2 - Написать характеристику партии Единая Россия ( обяз. пункты : по идеологическому...
2 - Дайте характеристику героям эпизода дети Арбата встречи Нового года с друзьями...
2 - Контрольна робота (1 семестр) 1 варіант Л. Християнські й язичницькі мотиви переплетено...
1 - На малюнку наведено процес в ідеальному газі в координатах Р(V). Перебудуйте...
3 - 1 Составь и реши задачу по таблице. у t A 1-я швея 2-я швея 1-я швея Одинаковое...
2 - Записать решение уравнений для всех токов в общем виде...
3 - Определить ускорения тел в приведенной системе . Массы тел одинаковы, коэффициент...
3
6
Объяснение:
Ограничения:
Замечаем, что первые два слагаемых имеют общую структуру в виде функции:
Действительно, если вместо t подставить x-2, то
Аналогично
Тогда 3-е слагаемое нашего уравнения представим в виде разности двух линейных функций вида: g(t)=at
Дополним g(t) к основной функции:
Исследуем ее на монотонность с производной
Заметим, что t²≥0; √(t²+1)>0, при любых действительных t, тогда
Значит f'(t)>0, следовательно f(t) - монотонно возрастающая функция на всей числовой оси
Для монотонных функций справедливо:
f(a)=f(b) ⇔ a=b
Перепишем наше уравнение в следующем виде