Решить уравнение: 2cos^2x+sinx+1=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание 2. Используйте пищевую сеть, чтобы ответить на следующие вопросы....
3 - Мұз араласқан салқын суды термосты ұзақ уақыт сақтауға болады ма?...
1 - Анализ1.Проанализируйте данные численности определённых гипотетических...
2 - Егер В, нүктесі В(1; -4) нүктесін: 1) жоғары қарай 3 бірлікке; 2)...
1 - . Центрі (x, y) иүктесінде жаткан, радиусы R шеңбердің теңдеуін жазындар:...
2 - русский язык упражнение 39в ,7 класс...
3 - «Құтты білік» дастанындағы автордың жаратқанға тәубе етуі шығарманың...
2 - -5,4 c (в кубе) x (в квадрате) +2,9 c (в кубе) х ( в квадрате) + 2,3...
3 - Почему в анкете Николка не указывает отчество?Шолохов Родинка...
2 - Румынский Афмитетр Пловдивы...
2
Объяснение:
Пусть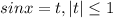 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Условию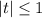 удовлетворяет t=-1.
удовлетворяет t=-1.