Решить уравнение 2 ^(x+1)+2^x> 6 решить уравнение 2 cos^2 x+3cosx-5=0

1) 

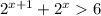
2) Область значений косинуса: -1 ≤ Cosx ≤ 1

2Cos²x + 3Cosx - 5 = 0

Если произвести замену и решить как обыкновенное квадратное уравнение

Cosx=a

2a² + 3a - 5 = 0

D = 49 ⇒ √D = 7

a₁ = 1

a₂ = -10/4 (не подходит, т.к. -1 ≤ Cosx ≤ 1)

Cosx = 1 ⇒ x = 2πk , k∈Z

ответ: x = 2πk

1)2^x+1+2^x>6

2^x*(2+1)>6.3*2^x>3*2,2^x>2x>1

2)2cos ²x+3cosx-5= 0

Пусть cosx= t, тогда уравнение примит вид: 

2t²+3t-5=0

D=9-4*2*(-5)=49; √49= 7

X1x2= -3±7/4; x₁=1, x₂= -5/2=-2,5

Вернемся к обозначению:

Cosx=-2,5, не может т.к соsx от промежутка [-1;1]

Cosx= 1

X=2πk, n∈ z

ответ: x= 2πk, n∈ z.