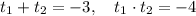Решить уравнение 10ый класс
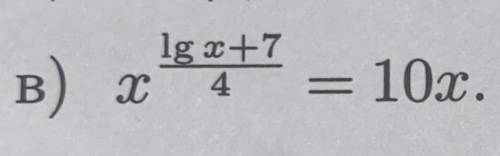
Другие вопросы по теме Алгебра
Популярные вопросы
- Четырехугольник ABCD – параллельная проекция ромба. Построить...
2 - Какая главная особенность погоды? Назовите элементы погоды?Как...
1 - Дайте определение образования слов и приведите примеры: - морфологический;...
2 - Запишите предложение, выделите в них грамматическую основу. 1)...
3 - Разбор текста январским утром...
3 - До ть Які реакції відносять до окисно- відновних...
2 - Востановить правильную последовательность событий сказки.первая...
3 - Город, пятый, синий, строить- это какие стили речи...
2 - Стр 62 упражнения 1 6-класс...
2 - .Отметьте вариант, в котором неверно указаны грамматические характеристики...
1
Объяснение:
по теореме Виета: