1. Алгебра
  2. Решить тригонометрическое уравнение

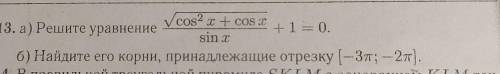
Решить тригонометрическое уравнение фото прилагается


Решить тригонометрическое уравнение фото прилагается

dkuchanov1352 dkuchanov1352    2   04.01.2022 02:24    1

Ответы
Ринатеовллктаоа Ринатеовллктаоа  04.01.2022 06:00

\frac{\sqrt{\cos^2(x)+\cos(x)}}{\sin(x)}+1 =0\\\left \{ {{\sqrt{\cos^2(x)+\cos(x)}=-\sin(x)} \atop {\sin(x) \neq 0}} \right.\\

Для решения воспользуемся равносильным переходом.

\sqrt{f(x)} = g(x) \left \{ {{f(x) = g^2(x)} \atop {g(x)\geq 0}} \right.

\\\left \{ {\cos^2(x)+\cos(x)=\sin^2(x)} \atop {\sin(x)

Решим первое уравнение системы и затем на тригонометрической окружности пересечем с неравенством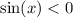 \sin(x) < 0 .

\cos(x)(2\cos(x)+1) = 0\\a) \cos(x) =0; x = \frac{\pi}{2}+\pi k ,k \in \mathbb{Z}\\b) 2\cos(x)+1 =0; \cos(x) = - \frac{1}{2}; x = ^+_- \frac{2\pi}{3} + 2\pi k, k \in \mathbb{Z}\\

*окружность с проверкой корней прикреплена*

Ans: \\x = \frac{4\pi}{3} + 2\pi k , k \in \mathbb{Z}\\x = \frac{3\pi}{2} + 2\pi k , k \in \mathbb{Z}


Решить тригонометрическое уравнение фото прилагается
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
SsuccesS SsuccesS  12.07.2019 02:00
А)постройте график функции у=1/3х-2 б)проходит ли график функции этой функции через точку к(-69; -21)?...
собакаАделет собакаАделет  12.07.2019 02:00
Решить уравнения: 1) 5³*х=5⁴ 2) х*3=3³ 3) 2 в пятой степени : х=2⁴ 4) х: 4=4³...
dmoro dmoro  12.07.2019 02:00
Найдите значение выражения x -4/x =3...
Anna19072003 Anna19072003  12.07.2019 02:00
Решить тригонометрические уравнения 1) cos^2(x)+sinx-1=0 2) sin5x*cosx+sinx*cos5x=1 3) 3sin-9cosx=0 4) sin2x+sinx=0 5) 3sin^2(7/2x)-cos^2(7/2)x=-1/2...
MELEKLER87 MELEKLER87  16.05.2019 14:12
1. выражение 2икс(2икс+3у)-(2+у)²2.решите систему уравнений4икс-у=93икс+7у=-1 скобку систему не нарисовала3.разложите на множителиа)3а²-9аб б)х³25хза ответ 40 надо...
MaarioForte MaarioForte  16.05.2019 14:12
Key m ows />1. выберите из пар чисел (2; — 1), (-1; 2) и (1; 1) ту, которая являетсяx+2y = 3,решением системы уравнений1 x +4y = 5.​...
alkozlovtzeva alkozlovtzeva  16.05.2019 14:11
Y=(x+4)^2 решите,найдите наименьшее и наибольшее значение я вам булочку с маком...
Ивангай228666 Ивангай228666  16.05.2019 14:09
При каком значении d система уравнений dx+2y=3, 5x+y= -4 и 7x+6y= -1 имеет единственное решение?...
RaspberryYogurt RaspberryYogurt  16.05.2019 14:08
Решить систему уравнений методом подстановки y=-3x 5x+3y=12...
daramir02 daramir02  16.05.2019 14:03
Скоратите дробь 33^n/3^n-1 * 11^n+1...

Популярные вопросы