Решить тригонометрическое уравнение: а) 2sinx+√2=0 б) sin3xcosx + cos3xsinx=0 в) cos6x=cos4x p.s я знаю что это элементарно, но грамотно составить и решить не
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему онегин принял вызов ленского на дуэль?...
3 - Волчье логово заменить на два существиельных...
1 - Составление прогноза изменения растительного мира. нужно. мне завтра !...
3 - 1+2x=10x+3 ; -4+3x=8x+5 ; 9+4x=8x-9 ; 2+8x=3x+9 ; 6-2x=3x-10 ; 5-2x=8x+9...
3 - Какое давление оказывает бетонная плита на пол если её толщина-30см...
3 - Что характерно для щитовника мужского и что отличаетт его от хвоща полевого?...
2 - Чем задние ноги лягушки отличаются от передних....
1 - Найдите углы прямоугольного треугольника,если один из них 30 градусов!...
3 - Модуль вектора р дорівнює 6 , а його координати рівні знайти координати...
2 - Решите .сегодня цена ботинок на 1_10(это дробь) меньше вчерашней цены.сколько...
2
1)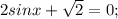
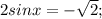
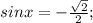
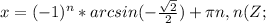
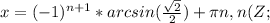
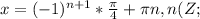
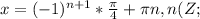 .
.
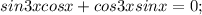
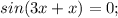
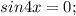
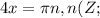
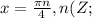
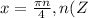 .
.
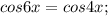
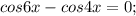
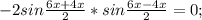
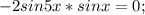
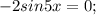
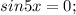
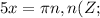
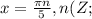
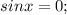
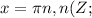
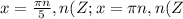 .
.
ответ:
2)
ответ:
3)
а)
б)
ответ: