Решить тригонометрическое уравнение.
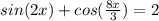
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужна ОБЯЗАТЕЛЬНО НУЖНО ОБЪЯСНИТЬ РАССТАНОВКУ ЗНАКОВ ПРЕПИНАНИЯ ...
1 - Н е е олице причины продвиласеверных гуннов (4 причины)1. Внутренние распри2.Экологические...
2 - Представь в виде степени 4=9*9*9*9=5*5*5*5*5=3*3*3*3*3*3*3=2*2*2*2*2*2*2*2=...
3 - Как решать рациональные неравенства? Можно кратко объяснить ...
2 - Синтаксический разбор предложения Смотровой окно от вредного солнечного излучения...
2 - КонгрессҒаламтордан кітапханасы туралы акпарат тауып оқыныз ( жоғарындағы сілтеме...
1 - перевестиАбай қазақтың жазба әдебиетінің негізін қалады. Ол қазақтың дәстүрліөлең...
3 - Найдите объем параллелепипеда...
2 - 1. Дана последовательность операторов: a:=1; b:=2; while a+b 8 do begin a:=a+1;...
3 - Характеры героев два еврея богатый и бедный...
2
так как максимальное значение синуса и косинуса равно 1, то левая сумма равна 2 только тогда оба слагаемых равны 1
sin(2x)=1; 2x=pi/2+2pik; x=pi/4+pik
cos(8x/3)=1; 8x/3=2pin; 8x=6pin; x=3pin/4 (k,n∈Z)
так как ищем х, одновременно подходящий обоим ответам
pi/4+pik=3pin/4
pi+4pik=3pin
1+4k=3n-решаю диофантовое уравнение
4k-3n=-1
k=2;n=3-частный случай, тогда общее решение имеет вид
k=2-3t; n=3-4t; t∈Z
x=3pin/4=3pi(3-4t)/4=9pi/4-3pit t∈Z