Решить тригонометрическое уравнение: 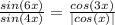
Другие вопросы по теме Алгебра
Популярные вопросы
- Тег (br) языка гипертекстовой разметки html означает: а) элемент маркированного...
3 - Решите уравнение , cosx=-3 корня из 2...
3 - Разобрать по членам предложения, определить падеж имён прилагательных. и...
1 - По картам атласа и учебника найдите водные системы равнины (волго – канал,...
2 - Периметр треугольника равен 156 см, а длины сторон относятся как 6: 9: 11....
3 - Эта духовная дочь протопопа аввакума во сне увидела его райскую палату...
1 - Смещение равновесия при повышении давления и понижения температуры...
2 - Найдите сумму величин и результат выразите натуральным числом, изменив единицу...
1 - В9 одинаковых банках помещается 27 л яблочного сока. сколько надо банок чтобы...
2 - Решение по в треугольнике abc bd-бисектриса ab-15см ad-3см cd-4см найти bd...
2
Раскрываем знак модуля:
Если cosx >0, то |cosx|=cosx
уравнение принимает вид:
По формуле произведения синуса на косинус:
тогда
По формуле разности синусов:
или
и
и
О т в е т первого случая c учетом cosx >0:
Если cosx <0, то |cosx|= - cosx
уравнение принимает вид:
По формуле синуса двойного угла
тогда
или
или
так как
и
и
О т в е т второго случая c учетом cosx <0
О т в е т. Объединяем ответы первого и второго случаев: