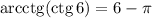Решить тождество с пояснением!
arcctg(ctg6)
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить общее сопротивление двух секций пускового реостата R1 = 4 Ом; R2 = 10...
1 - Ессе на тему бути громадянином держави це для 9 класса...
2 - Прямі A і B паралельні і перетнута їх січною лінія. Знайти кути які утворилися...
3 - Складіть історичний портрет Нестора Махна...
1 - На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите...
2 - 7. (2 б) Який розмір зображення дерева висотою 15 м на плівці фотоапарата, якщо...
1 - В равнобедренном треугольнике АВС точки Р и Т-середины боковых сторон AB и BC соответственно....
2 - Общественно политические взгляды правителей !...
3 - путем визначити період та частоту обертання барабану пральної машини або микрохвильової...
2 - Всем известен памятник Минину и Пожарскому, установленный на Красной площади в Москве...
2
Известно соотношение:
Кроме этого, известно, что основной период котангенса равен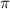 :
:
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида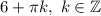 , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: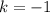 .
.
Запишем:
Действительно, , арккотангенс может принимать такое значение.
, арккотангенс может принимать такое значение.
ответ: