Алгебра: Решить содержащие корни высших степеней

1) Пусть .Заметим, что , так как корней на оси симметрии нет, то корней четное количество. Значит, либо их нет, либо их два. Нетрудно видеть, что - корень, а, значит, тоже.ответ: 4, -32) , здесь аналогично - ось симметрии , точно так же подбираем: , значит, - тоже корень.ответ: 2, 583) ; Теперь сгруппируем: , в итоге: , корни: 2, -1, но -1 не подходит, 2 подходит.ответ: 2...

Решить содержащие корни высших степеней

Ответы

Ленка111545 04.10.2020 13:10

$1. \sqrt[3]{5x+7}-\sqrt[3]{5x-12}=1$

делаем замену:

$\sqrt[3]{5x+7}=a \\\sqrt[3]{5x-12}=b$

избавляемся от корня:

$a^3=5x+7\\b^3=5x-12\\a^3-b^3=5x+7-5x+12\\a^3-b^3=19$

составляем систему и решаем ее:

$\left \{ {{a^3-b^3=19} \atop {a-b=1}} \right. \\\left \{ {{(a-b)(a^2+ab+b^2)=19} \atop {a=b+1}} \right. \\(b+1)^2+b(b+1)+b^2=19\\b^2+2b+1+b^2+b+b^2=19\\3b^2+3b=18\\b^2+b-6=0\\D=1+24=25=5^2\\b_1=\frac{-1+5}{2}=2 \\b_2=\frac{-1-5}{2}=-3\\a_1=2+1=3\\a_2=-3+1=-2$

подставляем значения a и b:

$1)a=3;b=2\\3^3=5x+7\\5x=20\\x=4\\2^3=5x-12\\5x=8+12\\5x=20\\x=4\\2)a=-2; b=-3\\-8=5x+7\\5x=-15\\x=-3\\-27=5x-12\\5x=-15\\x=-3$

В итоге получили два корня: -3 и 4

ответ: 4; -3

следущее уравнение решается аналогично.

$2. \sqrt[3]{x+6}+\sqrt[3]{66-x}=6\\\sqrt[3]{x+6}=a\\\sqrt[3]{66-x}=b\\a^3=x+6\\b^3=66-x\\a^3+b^3=72\\\left \{ {{a^3+b^3=72} \atop {a+b=6}} \right. \\\left \{ {{(a+b)(a^2-ab+b^2)=72} \atop {a+b=6}} \right. \\\left \{ {{a^2-ab+b^2=12} \atop {a=6-b}} \right. \\(6-b)^2-b(6-b)+b^2=12\\(b-6)^2+b(b-6)+b^2=12\\b^2-12b+36+b^2-6b+b^2=12\\3b^2-18b+24=0\\b^2-6b+8=0\\D=36-32=4=2^2\\b_1=\frac{6+2}{2} =4\\b_2=\frac{6-2}{2} =2\\a_1=6-4=2\\a_2=6-2=4$

$1)a=2;b=4\\x+6=8\\x=2\\66-x=64\\x=2\\2)a=4; b=2\\x+6=64\\x=58\\66-x=8\\x= 58$

ответ: 58; 2

$3. \sqrt{x+2}-\sqrt[3]{3x+2}=0\\\sqrt{x+2}=\sqrt[3]{3x+2}=0$

возводим обе части в шестую степень:

$(x+2)^3=(3x+2)^2\\x^3+6x^2+12x+8=9x^2+12x+4 \\x^3-3x^2+4=0$

не забываем, что по определению арифмитического квадратного корня:

$\left \{ {{x+2\geq 0} \atop {3x+2\geq 0}} \right. \\\left \{ {{x \geq -2} \atop {x \geq -\frac{2}{3} }} \right.\\x\in [-\frac{2}{3}; +\infty)$

продолжаем решать уравнение:

x^3-3x^2+4=0

корнями данного уравнения могут быть делители свободного члена:

$x=1\\1-3+4\neq 0\\x=2\\8-12+4=0$

один из корней уравнения: x=2

значит данное уравнение можно представить в виде произведения (x-2) на квадратный трехчлен:

$(x-2)(x^2+ax+b)=0\\x^3+ax^2+bx-2x^2-2ax-2b=0\\x^3+x^2(a-2)+x(b-2a)-2b=0$

приравняем коэффициенты:

$a-2=-3\\b-2a=0\\-2b=4\\a=-1\\b=-2\\$

получим:

$(x-2)(x^2-x-2)=0\\x^2-x-2=0\\D=1+8=9=3^2\\x_2=\frac{1+3}{2} =2\\x_3=\frac{1-3}{2} =-1 \notin [-\frac{2}{3}; +\infty)$

ответ: 2

ПОКАЗАТЬ ОТВЕТЫ

OkumRin 04.10.2020 13:10

1) Пусть $f(x)=\sqrt[3]{5x+7}-\sqrt[3]{5x-12}$ .

Заметим, что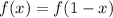 f(x)=f(1-x) , так как корней на оси симметрии нет, то корней четное количество. Значит, либо их нет, либо их два. Нетрудно видеть, что 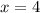x=4 - корень, а, значит, x=-3 тоже.

ответ: 4, -3

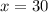2) $\sqrt[3]{x+6}+\sqrt[3]{66-x}=6$ , здесь аналогично - ось симметрии x=30 , точно так же подбираем: 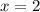x=2 , значит, 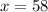x=58 - тоже корень.

ответ: 2, 58

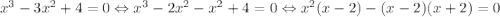3) $\sqrt{x+2}=\sqrt[3]{3x+2}\Rightarrow (x+2)^3=(3x+2)^2\Leftrightarrow x^3-3x^2+4=0$ ; Теперь сгруппируем: $x^3-3x^2+4=0\Leftrightarrow x^3-2x^2-x^2+4=0\Leftrightarrow x^2(x-2)-(x-2)(x+2)=0$ , в итоге: (x-2)(x^2-x-2)=0 , корни: 2, -1, но -1 не подходит, 2 подходит.