решить систему уравнений второй степени с двумя переменными сложения . и объяснить как решали
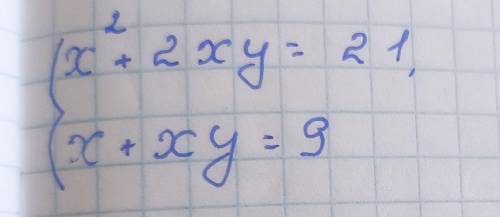
Другие вопросы по теме Алгебра
Популярные вопросы
- Формы настоящего времени образуются с личных окончаний глаголов правда или нет...
2 - Запишіть усі неправильні дроби зі чисельником 19, у яких чисельних і знаменник...
1 - Привести примеры из художественной литературы процессы экономических отношений?...
2 - Определите порядок реакции и рассчитайте, как изменится начальная скорость гомогенных...
2 - В состав океана входит остров 2) 7000 3) 5000 4). 3000...
3 - 1) 173232:48 2)216161:43 3) 975255:79 решите столбиком...
3 - Як залежить сила взаємодії між зарядами від відстані між ними...
1 - Как определить модуль силы упругости,чтобы понять куда напрвлен знак,для решения...
3 - Найдите угол ромба ABCD, если его диагонали AC и BD равны 6 м 6√3 м....
1 - Решите, что на фото: 4)найти уравнение плоскости ; 5) угол между ребром задача...
2
В решении.
Объяснение:
Решить систему уравнений второй степени с двумя переменными сложения.
х² + 2ху = 21
х + ху = 9
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно умножить второе уравнение на -2:
х² + 2ху = 21
-2х - 2ху = -18
Сложить уравнения:
х² - 2х + 2ху - 2ху = 21 - 18
Привести подобные:
х² - 2х - 3 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 4 + 12 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(2-4)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(2+4)/2
х₂=6/2
х₂= 3;
Теперь поочерёдно подставить значения х₁ и х₂ в любое из двух уравнений системы и вычислить у₁ и у₂:
а) х + ху = 9 х₁ = -1;
-1 - у = 9
-у = 9 + 1
-у = 10
у₁ = 10/-1
у₁ = -10;
б) х + ху = 9 х₂ = 3;
3 + 3у = 9
3у = 9 - 3
3у = 6
у₂ = 6/3
у₂ = 2;
Решения системы уравнений: (-1; -10); (3; 2).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
Объяснение:
Суммируем эти уравнения:
ответ: (-1;-10), (3;2).