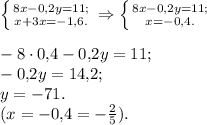Решить систему уравнений методом подстановки 3х+у=-6 и -4х+3у=0; методом сложения 9х-3у=-6 и -4х+3у=0;
методом сложения 2х+5у=8 и -4х+3у=7;
Методом подстановки 8х-0,2у=11 и х+3х=-1,6.
Другие вопросы по теме Алгебра
Популярные вопросы
- Добрые люди мне сделать СОЧ по Русскому языку 4 классесли что...
1 - Відносна густина деякого газу заповітрям 1,31. Яка маса 156,8...
3 - Дан треугольник abc с вершинами в точках a(1;-4;-1) b(4;7;0)...
2 - Решить уравнение: -1-х - - = - ответ перевести в 3 3 6 десятичную...
1 - Сила тертя ковзання при русі тіла дорівнює 30Н, а сила нормальної...
2 - Напишите уравнения химических реакций: а) получения фосфора из...
1 - ответ на во Назовите произведения, герои которых своим товарищам....
1 - Көмек ағылшын, 6сынып осыған көмек...
1 - Сколько воды можно нагреть от 20 С до 100 С и испарить за счет...
2 - в течении получаса, задание: найти нужную эпюру и расставить...
1
1)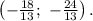
2)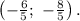
3)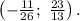
4)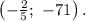
Объяснение:
1.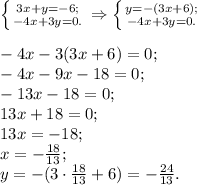
2.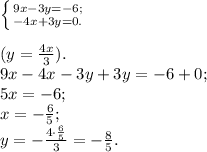
3.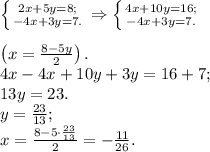
4.