Решить систему, через дискриминант!
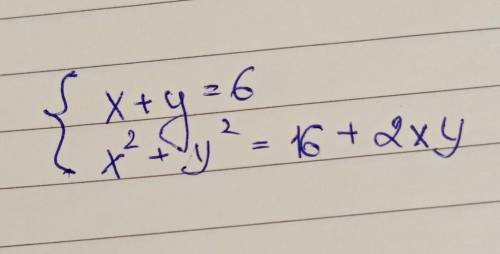
Другие вопросы по теме Алгебра
Популярные вопросы
- Составь предложение. Запиши его. Сделай разбор по членам и дай характеристику предложению....
2 - Реакция завершалась при 80 ° C за 18 мин. Сколько времени нужно, чтобы эта реакция...
1 - Во втором томе книги страниц больше на 20%, чем в первом томе. В третьем томе две...
3 - решить УМОЛЮЮЮЮЮЮЮЮ. Подсказка: Баку находится на 50°с.ш 40°в.д 3-ий часовой пояс...
1 - Выпишите основную причину наступления смуты Когда годунов царствовал 7 класс история...
3 - ОЧЕНЬ Учебник история нового времени 8кл, юдовская ВОПРОС : Докажите, используя...
2 - :С Заполни таблицу, если дана функция S(a)=a2 . Эта функция характеризует площадь...
2 - Будь ласочка дуже треба Унаслідок взаємодії 10,8 г невідомого алкіну з 8,96 л водню...
1 - Может ли шахматный конь обойти все клетки стандартной доски по одному разу, если...
1 - Задание №1. Выполните тест (пишите только цифру вопроса и букву правильного ответа) 1. ...
1
решаем квадратное уравнение:
подставляем в систему сначала одно значение:
(1; 5)
потом второе:
(5; 1)
ответ: (1; 5), (5; 1)